金融经济学 | 随记

CAPM理论

均值方差定义

均值
$\bar{r}=\frac{1}{N} \sum_{i=1}^N r_i=\mathrm E\left(\tilde r\right)$
方差
$\sigma^2=\frac{1}{N} \sum_{i=1}^N\left(r_i-\bar{r}\right)^2= \mathrm E\left(\tilde r-\bar r\right)^2$
标准差
\sigma=\sqrt{\frac{1}{N} \sum_{i=1}^N\left(r_i-\bar{r}\right)^2}
- 又叫波动率
协方差
$\sigma_{x y}=\frac{1}{N} \sum_{i=1}^N\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)= \mathrm E\left(\tilde x-\bar x\right)\left(\tilde y-\bar y\right)$
相关系数
$\rho_{x y}=\frac{\sigma_{x y}}{\sigma_x \sigma_y}$
这里都假设未来与过去的分布相同

均值方差特性

一种无风险资产和一种风险资产的组合
- 假设投在无风险资产和风险资产上的财富份额分别为 $1-w$ 与 $w$
  $\begin{aligned} & \bar{r}_p=E\left[(1-w) r_f+w \tilde r_s\right]=(1-w) r_f+w \bar{r}_s=r_f+w\left(\bar{r}_s-r_f\right) \\ & \sigma_p^2=E\left[(1-w) r_f+w \tilde r_s-(1-w) r_f-w \bar{r}_s\right]^2=E\left[w^2\left(\tilde r_s-\bar{r}_s\right)^2\right]=w^2\sigma_s^2\end{aligned}$
- 消去 $w$ 得到关于 $\bar{r}_p$ 和 $\sigma_p$ 的方程
  $\bar{r}_p=r_f+\frac{\bar{r}_s-r_f}{\sigma_s} \sigma_p$
两种风险资产的组合
\begin{cases} w_1+w_2=1 \\ \bar r=w_1 \bar r_1+w_2 \bar r_2 \\ \sigma^2=w_1^2 \sigma_1^2+w_2^2 \sigma_2^2+2w_1w_2 \sigma_{12} \end{cases}
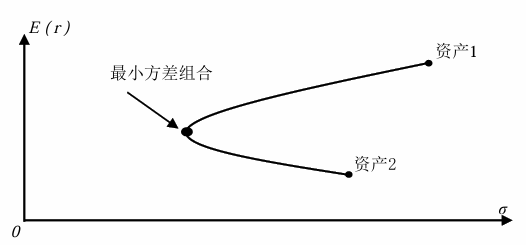
- 最小方差组合: 使得方差最小
  
  $\begin{align} &w_1^\ast=\frac{\sigma_2^2-\sigma_{12}}{\sigma_1^2+\sigma_2^2-2\sigma_{12}} \\ &w_2^\ast=\frac{\sigma_1^2-\sigma_{12}}{\sigma_1^2+\sigma_2^2-2\sigma_{12}} \\ &\bar r^\ast=\frac{\sigma_1^2\bar r_2+\sigma_2^2\bar r_1-\sigma_{12}(\bar r_1+\bar r_2)}{\sigma_1^2+\sigma_2^2-2\sigma_{12}} \end{align}$
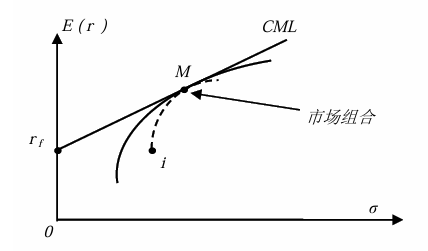
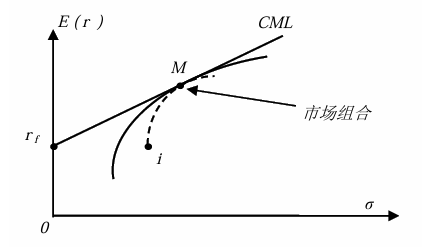
- 市场组合: 是有效前沿与经过无风险利率射线的切点
  
  $\begin{align} &w_1^\ast=\frac{\sigma_2^2(\bar r_1-r_f)-\sigma_{12}(\bar r_2-r_f)}{\sigma_1^2(\bar r_2-r_f)+\sigma_2^2(\bar r_1-r_f)-\sigma_{12}(\bar r_1+\bar r_2-2r_f)} \\ &w_2^\ast=\frac{\sigma_1^2(\bar r_2-r_f)-\sigma_{12}(\bar r_1-r_f)}{\sigma_1^2(\bar r_2-r_f)+\sigma_2^2(\bar r_1-r_f)-\sigma_{12}(\bar r_1+\bar r_2-2r_f)} \\ &\bar r^\ast=\frac{\sigma_1^2(\bar r_2-r_f)\bar r_2+\sigma_2^2(\bar r_1-r_f)\bar r_1-\sigma_{12}[(\bar r_2-r_f)\bar r_1+(\bar r_1-r_f)\bar r_2]}{\sigma_1^2(\bar r_2-r_f)+\sigma_2^2(\bar r_1-r_f)-\sigma_{12}(\bar r_1+\bar r_2-2r_f)} \end{align}$
多种风险资产组合的有效前沿
- 开口向右、上下对称的双曲线。上半边称为投资组合的“有效前沿”
- 最小方差组合
  $\min_{w_1,\cdots,w_n} \sum_{i=1}^n w_i^2\sigma_i^2 \quad\mathrm{s.t.}\quad\begin{cases} \sum_{i=1}^n w_i=1 \\ \sum_{i=1}^n w_i \bar r_i=\bar r \end{cases}$
共同基金定理
- 存在无风险资产时: 偏好只影响无风险资产和市场组合之间的配置权重，不影响市场组合的构成。投资经理基于各种风险资产的收益风险特性，构建出“市场组合”，再根据客户的偏好，将客户的资产在无风险资产和市场组合之间做配置
- 不存在无风险资产时: 任何有效前沿上的组合均可以由两个处在有效前沿上的组合得到。投资者要做的，只是找到两个处在有效前沿上的投资组合，然后按
  照自己的风险偏好在这两者之间做配置即可

CAPM推导

基于效用函数的CAPM论证
- 假设投资者的效用函数为
  $u(\tilde r)=\bar r - A\sigma^2$
- 假设投资 $w$ 于资产 $i$ 、 $1-w$ 于市场组合 $M$ ，则效用为
  $\begin{align} u(\tilde r_p)&=\bar r_p - A\sigma^2_{p} \\ &=[w\bar r_i+(1-w)\bar r_M]-A[w^2\sigma_i^2+(1-w)^2\sigma_M^2+2w(1-w)\sigma_{iM}] \end{align}$
- 均衡时，效用对 $w$ 的导数恒等于0
  $\frac{\mathrm d u}{\mathrm d w}=\bar r_i-\bar r_M-2Aw(\sigma_i^2+\sigma_M^2-2\sigma_{iM})-2A(\sigma_{iM}-\sigma_M^2)\equiv 0$
- 由于是恒等式，可以左右同时代入 $w=0$ ，得到式（1）
  $\bar r_i-\bar r_M-2A(\sigma_{iM}-\sigma_M^2)\equiv 0$
- 由于式（1）是恒等式，可以左右同时代入 $\tilde r_i=r_f$
  $r_f-\bar r_M-2A\sigma_M^2\equiv 0\quad\Rightarrow\quad A=\frac{r_f-\bar r_M}{2\sigma_M^2}$
- 由于式（1）是恒等式，可以左右同时代入 $A=\frac{r_f-\bar r_M}{2\sigma_M^2}$
  $\bar r_i-\bar r_M-\frac{r_f-\bar r_M}{\sigma_M^2}(\sigma_{iM}-\sigma_M^2)$
- 化简后得到 $\bar r_i= r_f+\frac{\sigma_{iM}}{\sigma_M^2}(\bar r_M-r_f)$
基于组合构建的CAPM论证
- 假设投资 $w$ 于资产 $i$ 、 $1-w$ 于市场组合 $M$ ，则收益率的期望与标准差分别为
  $\begin{align} \bar r_p&=w\bar r_i+(1-w)\bar r_M=w(\bar r_i-\bar r_M)+\bar r_M \\ \sigma_p&=\sqrt{w^2\sigma_i^2+(1-w)^2\sigma_M^2+2w(1-w) \sigma_{i M}} \\ &=\sqrt{w^2\left(\sigma_i^2+\sigma_M^2-2\sigma_{i M}\right)+2w\left(\sigma_{i M}-\sigma_M^2\right)+\sigma_M^2} \end{align}$
- 由于CML线与有效前沿相切于市场组合 $M$ ，因此也一定相切于 $M$ 和资产 $i$ 构成的有效前沿
- 因此曲线 $\stackrel\frown{Mi}$ 在 $M$ 点的斜率恒等于CML线的斜率
  $\frac{\mathrm d \bar r_p}{\mathrm d \sigma_p}\equiv\frac{\bar r_M-r_f}{\sigma_M}$
- 由于是恒等式，可以左右同时代入 $w=0$
  $\frac{\bar r_M-r_f}{\sigma_M}\equiv \left.\frac{\mathrm d \bar r_p}{\mathrm d \sigma_p}\right|_{w=0}=\frac{\left.\frac{\mathrm d \bar r_p}{\mathrm d w}\right|_{w=0}}{\left.\frac{\mathrm d \sigma_p}{\mathrm d w}\right|_{w=0}}=\frac{\bar r_i-\bar r_M}{\frac{\sigma_{iM}-\sigma_M^2}{\sigma_M}}$
- 化简后得到 $\bar r_i= r_f+\frac{\sigma_{iM}}{\sigma_M^2}(\bar r_M-r_f)$

SML和CML

推导方式
- 证券市场线CML: 使用无风险资产和风险资产 $i$ 构成不同组合，得到组合收益率与组合标准差的关系（见第5讲）
- 资本市场线SML: 对于风险资产 $i$ ，根据CAPM方程，其收益率与 $\beta_i$ 的关系（见第6讲）
相似点
- 都是期望收益率 = 无风险利率 + 风险的度量 × 风险的价格的形式
  $\begin{align} &\bar{r}_p=r_f+ \sigma_p\times \frac{\bar{r}_i-r_f}{\sigma_i} \\ &\bar r_i= r_f+\beta_i\times(\bar r_M-r_f) \end{align}$
不同点
- CML: 对于不同风险资产 $i$ ，有不同的CML式（截距相同但斜率不同）
- SML: 不同风险资产 $i$ ，都遵循同一个SML方程

期望效用理论

期望效用定义

期望效用函数
U(\tilde y)=\mathrm E[u(\tilde y)]
- 离散形式: $U(\tilde y)=\sum \pi_iu(y_i)$
- 效用函数性质: $u^{\prime}(y)\gt0,u^{\prime\prime}(y)\lt0$
人性不耐
- 不同时刻期望效用函数相加
  $U=U_0+\delta_1U_1+\cdots+\delta_nU_n$
- 其中 $\delta_n\lt\cdots\lt\delta_1\lt 1$ ，表示未来时刻的效用折现到现在
确定性等价
\mathrm E[u(\tilde y)]=u(y^\ast)
- $y^\ast$ 为常数，称为 $\tilde y$ 的确定性等值
风险厌恶系数
- 绝对风险厌恶系数ARA
  $R_A(y)=-\frac{u^{\prime\prime}(y)}{u^\prime(y)}$
- 相对风险厌恶系数RRA
  $R_R(y)=-\frac{yu^{\prime\prime}(y)}{u^\prime(y)}=yR_A(y)$
审慎系数
- 绝对审慎系数
  $P_A(y)=-\frac{u^{\prime\prime\prime}(y)}{u^{\prime\prime}(y)}$
- 相对审慎系数
  $P_R(y)=-\frac{yu^{\prime\prime\prime}(y)}{u^{\prime\prime}(y)}=P_A(y)$

投资储蓄行为

假设初始财产 $y$ ，拿出 $a$ 投资于收益率分布为 $\tilde r$ 的风险资产，则初始时刻与投资收回时刻的资产分别为
$\begin{align} &y_0=y-a \\ &\tilde y_1=a(1+\tilde r) \end{align}$
若只关注最终总的资产，效用为
$U=\mathrm E[u(y_0+\tilde y_1)]$
若分别考虑两时刻，总效用为
$U=\mathrm E[u(y_0)]+\delta_1 \mathrm E[u(\tilde y_1)]=u(y_0)+\delta_1 \mathrm E[u(\tilde y_1)]$

完备市场的均衡

符号定义
- 资本市场
  假设市场中有 $1$ 到 $J$ 种资产，下一时刻有 $1$ 到 $S$ 种状态。资产 $\boldsymbol{x}^j$ 使用 $x_s^j$ 表示 $s$ 状态下 $j$ 资产的支付
  $\boldsymbol{x}^j=\begin{bmatrix} x_1^j&\cdots&x_S^j \end{bmatrix}^\top$
  全部资产构成支付矩阵 $\boldsymbol{x}$ ，当 $\mathrm{rank}(\boldsymbol{x})=S$ 时市场完备
  $\boldsymbol{x}=\begin{bmatrix} \boldsymbol{x}^1&\cdots&\boldsymbol{x}^J \end{bmatrix}=\begin{bmatrix} x_1^1& \cdots & x_1^J \\ \vdots & \ddots & \vdots \\ x_S^1& \cdots & x_S^J \end{bmatrix}$
  资产组合 $\boldsymbol{\theta}$ ，使用 $\theta_j$ 表示对资产 $j$ 持有数量
  $\boldsymbol{\theta}=\begin{bmatrix} \theta_1&\cdots&\theta_J \end{bmatrix}^\top$
  期初价格 $\boldsymbol{p}$ ，使用 $p_j$ 表示对资产 $j$ 的期初价格
  $\boldsymbol{p}=\begin{bmatrix} p_1&\cdots&p_J \end{bmatrix}$
  则组合 $\boldsymbol{\theta}$ 的期初价格为 $\boldsymbol{p}\boldsymbol{\theta}$ ，下一时刻不同状态的支付为 $\boldsymbol{x}\boldsymbol{\theta}$
- 完备市场
  在完备市场中，给定任意消费计划 $\boldsymbol{c}=\begin{bmatrix}c_1&\cdots&c_S\end{bmatrix}^\top$ ，都能找到 $\boldsymbol{\theta}$ 使得支付等于 $\boldsymbol{c}$
  $\boldsymbol{x}\boldsymbol{\theta}=\boldsymbol{c}$
  定义只有在状态 $s$ 支付1，其他状态支付0的资产为阿罗证券 $\boldsymbol{I}_s$
  $\boldsymbol{I}_s=\begin{bmatrix}0&\cdots&1&\cdots&0\end{bmatrix}^\top$
  其价格 $\varphi_s$ 称为 $s$ 的状态价格
  $\begin{align} &\boldsymbol{\varphi}=\begin{bmatrix}\varphi_1&\cdots&\varphi_S\end{bmatrix} \\ &\boldsymbol{\varphi}\boldsymbol{x}^j=p_j\quad\boldsymbol{\varphi}\boldsymbol{x}=\boldsymbol{p} \end{align}$
  无风险资产期初价格 $\rho=\boldsymbol{\varphi}\boldsymbol{1}=\sum_{s=1}^S\varphi_s$
完备市场的一般均衡
- 单个消费者的均衡
  期初消费为 $c_0$ ，下一时刻消费的分布为 $\tilde c_1:P(\tilde c_1=c_s)=\pi_s\quad (s=1,2,\cdots,S)$ ，消费者的期望效用为
  $U=\mathrm E(u(c_0))+\delta\mathrm E[u(\tilde c_1)]=u(c_0)+\delta\sum_{s=1}^S \pi_s u( c_s)$
  假设消费者期初和下一时刻 $s$ 状态的禀赋为 $e_0,e_1,\cdots,e_S$ ，并且期初购买资产组合 $\boldsymbol{\theta}$ ，下一时刻出售，则消费量为
  $\begin{align} &c_0=e_0-\boldsymbol{p}\boldsymbol{\theta} \\ &c_s=e_s+\boldsymbol{I}_s^\top\boldsymbol{x}\boldsymbol{\theta}\quad\quad(s=1,\cdots,S) \end{align}$
  为简化处理，将购买的资产组合 $\boldsymbol{\theta}$ 分解为由阿罗证券构成的资产组合 $\boldsymbol{\vartheta}=\begin{bmatrix}\vartheta_1&\cdots&\vartheta_S\end{bmatrix}^\top$
  $\begin{cases} &c_0=e_0-\boldsymbol{\varphi}\boldsymbol{\vartheta} \\ &c_s=e_s+\vartheta_s\quad\quad(s=1,\cdots,S) \end{cases}\quad\Rightarrow\quad c_0+\sum_{s=1}^S\varphi_s(c_s-e_s)=e_0$
  至此得到消费者的期望效用与约束条件
  $\max_{c_0,c_1,\cdots,c_S} u(c_0)+\delta\sum_{s=1}^S \pi_s u( c_s)\quad\mathrm{s.t.}\quad c_0+\sum_{s=1}^S\varphi_s c_s=e_0+\sum_{s=1}^S\varphi_s e_s$
  或者写成向量形式
  $\max_{c_0,\boldsymbol c} u(c_0)+\delta\boldsymbol{\pi} u(\boldsymbol c)\quad\mathrm{s.t.}\quad c_0+\boldsymbol \varphi\boldsymbol c=e_0+\boldsymbol \varphi\boldsymbol e$
  其中
  $\boldsymbol c=\begin{bmatrix}c_1&\cdots&c_S\end{bmatrix}^\top$
  $\boldsymbol \pi=\begin{bmatrix}\pi_1&\cdots&\pi_S\end{bmatrix}$
  $\boldsymbol e=\begin{bmatrix}e_1&\cdots&e_S\end{bmatrix}^\top$
- 市场出清约束
  全部 $K$ 个消费者达到均衡，解出 $c_{k,s}=c_{k,s}(\varphi_1,\cdots,\varphi_S)$ ，但还不足以求解。因此假设消费力不能储藏，则还有下述条件
  $\sum_{k=1}^K c_{k,s}=\sum_{k=1}^K e_{k,s}\quad\quad (s=0,1,\dots,S)$
  这是因为不能储藏消费力时，消费者当期的剩余禀赋必须全部用于当期的消费，且消费者相互买卖资产 $x_j$ 只是交换禀赋不影响总禀赋，因此任意时刻和状态下，总消费等于总禀赋。最终求解出全部 $\varphi_i$ 以及 $c_{k,s}$
- 一般均衡下的资源分配是帕累托最优的，这被称为福利经济学第一定理
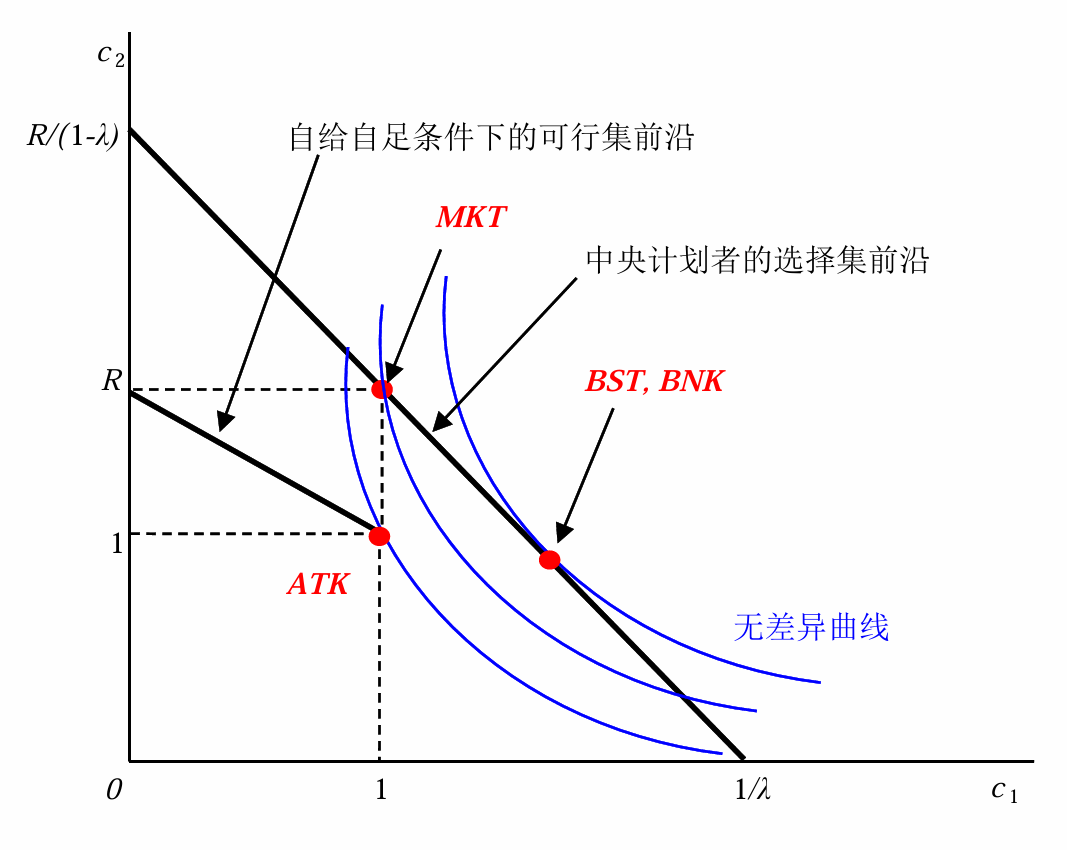
有中央计划者的完备市场
- 存在中央计划者时，直接调控 $c_{k,s}$ 实现效用最大化，因此不再是对每个消费者分别求均衡，而是直接写出总效用求解最大化
  $U=\sum_{k=1}^K\mu_k\left[u_k(c_{k,0})+\delta_k\sum_{s=1}^S \pi_s u_k( c_{k,s})\right]$
  $\mu_k$ 为消费者 $k$ 的权重，满足 $\sum_{k=1}^K \mu_k=1$
- 由于不再是对每个消费者分别求均衡，因此只剩市场出清的约束条件，效用最大化均衡为
  $\max_{\{c_{k,0},\cdots,c_{k,S}\}_{k=1}^K} \sum_{k=1}^K\mu_k\left[u_k(c_{k,0})+\delta_k\sum_{s=1}^S \pi_s u_k( c_{k,s})\right]\quad\mathrm{s.t.}\quad\sum_{k=1}^K c_{k,s}=\sum_{k=1}^K e_{k,s}\quad (s=0,1,\dots,S)$
  还需要额外条件求解，最优分配下对于每个消费者有
  $\sum_{s=1}^S(c_{k,s}-e_{k,s})\pi_s u^{\prime}_k(c_{k,s})=0\quad(k=1,\cdots,K)$
- 显然，存在中央计划者时的总效用不小于一般均衡时的总效用，当初始财富分布满足一定条件时，二者取等。因此，中央计划者可以通过调整期初财富分配，然后让消费者自发达成一般均衡，同样能实现总效用最大化，这被称为福利经济学第二定理

DD银行模型

设定
- 存在 $t=0,1,2$ 三个时刻， $t=0$ 时刻获得一单位消费品，之后不再获得
- 消费品有两种用途，消费或投资，其中投资分为两种
  短期投资: 将 $t$ 时刻1单位消费品转换为 $t+1$ 时刻1单位消费品
  长期投资: 将 $t=0$ 时刻1单位消费品转换为 $t=2$ 时刻R单位消费品，不能在 $t=1$ 时刻提取
  $t=0$ 时刻，消费者将 $1-\theta$ 份额的消费品用于长期投资
- 消费者分为前期消费者和后期消费者
  前期消费者: $\lambda$ 可能性，只能从1时刻的消费获得效用
  后期消费者: $1-\lambda$ 可能性，只能从2时刻的消费获得效用
  $t=1$ 时刻，消费者得知自己的类型
- 效用函数为
  $EU=\lambda u(c_1)+(1-\lambda)u(c_2)$
自给自足状况下的配置
- $t=1$ 时刻，若发现自己为前期消费者，会将短期投资全部消费；反之等到 $t=2$ 时刻全部消费短期投资与长期投资
  $\begin{cases} c_1=\theta \\ c_2=\theta+(1-\theta) R \end{cases}$
- 效用函数与均衡
  $\max_\theta \lambda u(\theta)+(1-\lambda)u(\theta+(1-\theta) R)\quad\Rightarrow\quad \lambda u^\prime(\theta^{ATK})=(1-\lambda)(R-1)u^\prime(\theta^{ATK}+(1-\theta^{ATK}) R)$
- 记此时的期望效用为 $EU^{ATK}$ ，两时刻的消费满足
  $\lambda u^\prime(c_1^{ATK})=(1-\lambda)(R-1)u^\prime(c_2^{ATK})$
最佳配置（中央计划者配置）
- 假设人数 $N$ 足够大，根据大数定律，有 $\lambda N$ 人是前期消费者、 $(1-\lambda) N$ 人是后期消费者，于是按照这个比例配置投资
  $\begin{cases} \lambda N c_1=\theta N \\ (1-\lambda) N c_2=(1-\theta) RN \end{cases}$
- 效用函数与均衡
  $\max_\theta \lambda u\left(\frac{\theta}{\lambda}\right)+(1-\lambda)u\left(\frac{1-\theta}{1-\lambda} R\right)\quad\Rightarrow\quad u^\prime\left(\frac{\theta^{BST}}{\lambda}\right)=u^\prime\left(\frac{1-\theta^{BSK}}{1-\lambda} R\right)R$
- 记此时的期望效用为 $EU^{BST}$ ，两时刻的消费满足
  $u^\prime(c_1^{BST})=u^\prime(c_2^{BST})R$
- 银行与最佳配置相同， $EU^{BNK}=EU^{BST},c_1^{BNK}=c_1^{BST},c_2^{BNK}=c_2^{BST}$
市场均衡
- 假设 $t=1$ 时刻，消费者可以在市场中交易投资，将1单位长期投资转换为p单位短期投资或相反，因此
  $\begin{cases} c_1=\theta+(1-\theta)p \\ c_2=\left(1-\theta+\frac{\theta}{p}\right) R \end{cases}$
- 均衡时， $p$ 一定等于1
  若 $p\gt 1$ ，消费者会不考虑短期投资，短期投资减少，长期投资能够兑换短期资产的数量 $p$ 下降趋向 $0$
  若 $p\lt 1$ ，消费者会不考虑长投资，长期投资减少，长期投资能够兑换短期资产的数量 $p$ 上升趋向 $R$
  于是
  $\begin{cases} c_1=1 \\ c_2= R \end{cases}$
- 效用为
  $EU^{MKT}=\lambda u(c_1^{MKT})+(1-\lambda)u(c_2^{MKT})$
  其中 $c_1^{MKT}=1,c_2^{MKT}=R$
不同条件下的均衡期望效用

C-CAPM理论

随机折现

考虑消费者优化问题
- 给定所有资产的持有量 $\boldsymbol \theta=\begin{bmatrix}\theta_1&\cdots&\theta_J\end{bmatrix}^\top$ ，使得效用最大化
  $\max_{\boldsymbol \theta} u(c_0)+\delta\boldsymbol{\pi} u(\boldsymbol c)\quad\mathrm{s.t.}\quad\begin{cases} c_0=e_0-\boldsymbol{p}\boldsymbol{\theta} \\ \boldsymbol c= \boldsymbol e+\boldsymbol{x}\boldsymbol{\theta} \end{cases}$
- 代入约束条件消去 $c_0,\boldsymbol{c}$
  $\max_{\boldsymbol \theta} u(e_0-\boldsymbol{p}\boldsymbol{\theta})+\delta\boldsymbol{\pi} u(\boldsymbol e+\boldsymbol{x}\boldsymbol{\theta})$
- 对 $\boldsymbol \theta$ 求导为 $\boldsymbol 0$
  $\frac{\partial}{\partial \boldsymbol\theta}\left[u(e_0-\boldsymbol{p}\boldsymbol{\theta})+\delta\boldsymbol{\pi} u(\boldsymbol e+\boldsymbol{x}\boldsymbol{\theta})\right]=-\boldsymbol{p}^\top u^\prime(e_0-\boldsymbol{p}\boldsymbol{\theta})+\delta\boldsymbol{x}^\top\mathrm{diag}(\boldsymbol{\pi})u^\prime(\boldsymbol e+\boldsymbol{x}\boldsymbol{\theta})=\boldsymbol 0$
- 即
  $\begin{align} &\boldsymbol{p}^\top u^\prime(c_0)=\delta\boldsymbol{x}^\top\mathrm{diag}(\boldsymbol{\pi})u^\prime(\boldsymbol c) \\ &p_j u^\prime(c_0)=\delta \sum_{s=1}^S\pi_su^\prime(c_s)x_s^j \end{align}$
- 将等号左边除过去
  $1=\delta \sum_{s=1}^S\pi_s\frac{u^\prime(c_s)}{u^\prime(c_0)} \frac{x_s^j}{p_j}=\delta \sum_{s=1}^S\pi_s\frac{u^\prime(c_s)}{u^\prime(c_0)}(1+r_{j,s})=\mathrm E\left[\delta\frac{u^\prime(\tilde c_1)}{u^\prime(c_0)}(1+\tilde r_j) \right]$
- 其中 $\tilde r_j$ 为资产 $j$ 下一时刻收益率的分布
随机折现因子
- 定义随机折现因子
  $\tilde m=\delta\frac{u^\prime(\tilde c_1)}{u^\prime(c_0)}$
- 于是公式化简为
  $\mathrm E\left[\tilde m(1+\tilde r_j) \right]=1$
- 称其为资产定价方程
代表性消费者与加总
- 不同消费者存在不同的效用函数 $u$ ，这会导致涉及效用函数的结论难以从个体消费者推广到整个市场
- 使用代表性消费者表示整个市场的消费者，其效用函数是所有消费者效用函数的某种平均，这样只需要考虑一个效用函数
- 代表性消费者的成立需要一定前提条件，假设前提条件都满足，这样个体消费者的效用函数相关结论能直接推广到整个市场

C-CAPM定价方程

推导
- 易证明，不同资产的线性组合也满足资产定价方程，再假设市场完备，则可以构造无风险资产，因此
  $\begin{cases} \mathrm E\left[\tilde m(1+ r_f) \right]=1 \\ \mathrm E\left[\tilde m(1+\tilde r_j) \right]=1 \end{cases}\quad\Rightarrow\quad \begin{cases} \mathrm E(\tilde m)=\frac{1}{1+r_f} \\ \mathrm E\left[\tilde m(\tilde r_j-r_f) \right]=0 \end{cases}$
- 根据协方差的性质
  $\mathrm{Cov}(\tilde m,\tilde r_j-r_f)=\mathrm E[\tilde m(\tilde r_j-r_f)]-\mathrm E(\tilde m)\mathrm E(\tilde r_j-r_f)$
- 代入 $E\left[\tilde m(\tilde r_j-r_f) \right]=0$ ，整理得到
  $\mathrm{Cov}(\tilde m,\tilde r_j)=-\mathrm E(\tilde m)\mathrm E(\tilde r_j-r_f)\quad\Rightarrow\quad \mathrm E(\tilde r_j)-r_f=-(1+r_f)\mathrm{Cov}(\tilde m,\tilde r_j)$
- 代回随机折现因子
  $\mathrm E(\tilde r_j)-r_f=-(1+r_f)\mathrm{Cov}\left[\delta\frac{u^\prime(\tilde c_1)}{u^\prime(c_0)},\tilde r_j\right]=-\frac{\delta(1+r_f)}{u^\prime(c_0)}\mathrm{Cov}\left[u^\prime(\tilde c_1),\tilde r_j\right]$
- 由于 $\tilde r_j=\frac{\tilde x_j}{p_j}-1$ ，根据未来价格分布 $\tilde x_j$ 计算资产价格 $p_j$
  $p_j=p_j \mathrm E\left[\tilde m(1+\tilde r_j) \right]=\mathrm E\left[\tilde m p_j(1+\tilde r_j) \right]=\mathrm E\left(\tilde m \tilde x_j \right)$
C-CAPM与CAPM
- 的CAPM事实上只是C-CAPM的一个特例，假设效用函数为二次型 $u(c)=-ac^2+bc$ ，则
  $\mathrm E(\tilde r_j)-r_f=\frac{2a\delta(1+r_f)}{b-2ac_0}\mathrm{Cov}\left(\tilde c_1,\tilde r_j\right)$
- 定义市场组合回报率 $\tilde r_M$ 。由于是完备市场，总能构造出这样的资产
  $\tilde r_M=\frac{\tilde c_1}{p_M}-1$
- 代入得到
  $\mathrm E(\tilde r_j)-r_f=\frac{2a\delta(1+r_f)p_M}{b-2ac_0}\mathrm{Cov}\left(\tilde r_M,\tilde r_j\right)$
- 该等式对市场组合也成立，于是
  $\begin{cases} \mathrm E(\tilde r_M)-r_f=\frac{2a\delta(1+r_f)p_M}{b-2ac_0}\mathrm{Var}\left(\tilde r_M\right) \\ \mathrm E(\tilde r_j)-r_f=\frac{2a\delta(1+r_f)p_M}{b-2ac_0}\mathrm{Cov}\left(\tilde r_M,\tilde r_j\right) \end{cases}\quad\Rightarrow\quad \frac{\mathrm E(\tilde r_j)-r_f}{\mathrm E(\tilde r_M)-r_f}=\frac{\mathrm{Cov}\left(\tilde r_M,\tilde r_j\right)}{\mathrm{Var}\left(\tilde r_M\right)}$
- 整理后得到CAPM公式。由此我们可以得到，市场组合是收益率分布等于消费增长率分布的组合，或者说，市场组合就是整个宏观经济

关于C-CAPM的讨论

变量间的关系
- 在一般均衡中，所有因素都相互影响，任意两个内生变量之间都存在着双向的因果关系
- 因此 $\tilde m,\tilde c_1,\tilde r_j,\tilde x_j$ 都存在相关关系，不能假设调整其中一个变量只会影响另一个变量
期望回报的决定
- 将期望回报分解为无风险利率和风险溢价两部分
  $\mathrm E(\tilde r_j)=r_f+[\mathrm E(\tilde r_j)-r_f]$
- 无风险利率的决定
  定义消费增长率 $\tilde g$
  $\tilde g=\frac{\tilde c_1}{c_0}-1$
  则无风险利率近似为
  $r_f\approx \frac{1-\delta}{\delta}+R_R\mathrm E(\tilde g)-\frac{1}{2}R_RP_R\mathrm{Var}(\tilde g)=\rho+R_R\bar g-\frac{1}{2}R_RP_R\sigma_g^2$
  $\rho$ 称为主观贴现率，反应消费者的人性不耐
  $R_R\bar g$ 反应经济增长，当经济增长越快，储蓄越不必要，无风险利率增加
  $\frac{1}{2}R_RP_R\sigma_g^2$ 反应预防性储蓄，经济增长波动越大，储蓄越有必要，无风险利率降低
- 风险溢价的决定
  $\mathrm E(\tilde r_j)-r_f=-\frac{\delta(1+r_f)}{u^\prime(c_0)}\mathrm{Cov}\left[u^\prime(\tilde c_1),\tilde r_j\right]$
  回报率与边际效用相关性越强的资产， $\mathrm{Cov}\left[u^\prime(\tilde c_1),\tilde r_j\right]$ 越大，风险溢价越小
  这表示消费欲望高（因为此时边际效用高）时该资产回报也高，这种资产当然风险溢价小、价格高
为什么存在交易
- 投资者买卖资产的目的是通过调整消费在不同时间、不同状态下的分布来最大化自己的效用
- 因此，从效用角度来说，资产交易不是零和博弈，而是资源在不同消费者之间进行优化配置的过程

定价理论

APT理论

C-CAPM与APT的对比
- C-CAPM为均衡资产定价，属于结构化模型(Structural Form)
- APT为无套利定价，更偏向简化式模型(Reduced Form)
APT的内容
- 因子组合: 因子载荷为1的资产组合
  $\tilde r_{pi}=r_f+\lambda_i-\mathrm E(\tilde f_i)+\tilde f_i$
- 因子溢价: 因子组合的风险溢价
  $\lambda_i=\mathrm E(\tilde r_{pi})-r_f$
- 任意资产的回报
  $\tilde r_i=\alpha_i+\sum\beta_i\tilde f_i\quad\Rightarrow\quad \mathrm E(\tilde r_i)=r_f+\sum\beta_i\lambda_i$

无套利定价理论

套利分类
- 第一类套利: 成本为负，收入为0
  $\boldsymbol{p}\boldsymbol{\theta}\lt0,\boldsymbol{x}\boldsymbol{\theta}=\boldsymbol0$
- 第二类套利: 成本为0，收入为正
  $\boldsymbol{p}\boldsymbol{\theta}=0,\boldsymbol{x}\boldsymbol{\theta}\gt\boldsymbol0$
- 第三类套利: 成本为负，收入为正
  $\boldsymbol{p}\boldsymbol{\theta}\lt0,\boldsymbol{x}\boldsymbol{\theta}\gt\boldsymbol0$
定义
- 资产支付
  $\boldsymbol{x}=\begin{bmatrix}x_1&\cdots&x_S\end{bmatrix}^\top$
- 状态价格向量
  $\boldsymbol{\varphi}=\begin{bmatrix}\varphi_1&\cdots&\varphi_S\end{bmatrix}$
  根据阿罗证券相关知识可知资产价格为 $p= \boldsymbol{\varphi} \boldsymbol{x}$
- 物理概率
  $\boldsymbol{\pi}=\begin{bmatrix}\pi_1&\cdots&\pi_S\end{bmatrix}$
- 状态价格密度
  $\boldsymbol{m}=\begin{bmatrix}\frac{\varphi_1}{\pi_1}&\cdots&\frac{\varphi_S}{\pi_S}\end{bmatrix}$
  $\boldsymbol{m}$ 是随机折现因子 $\tilde m$ 的离散形式，满足了
  $p=\sum_{s=1}^S \varphi_s x_s=\sum_{s=1}^S \pi_s m_s x_s=\mathrm E^{\pi}(\tilde m \tilde x)$
- 风险中性概率
  $\boldsymbol{q}=\frac{\boldsymbol{\varphi}}{\sum_{s=1}^S \varphi_s}=e^{r_f}\boldsymbol{\varphi}$
- 风险中性定价
  $p=\boldsymbol{\varphi}\boldsymbol{x}=e^{-r_f}\boldsymbol{q}\boldsymbol{x}=e^{-r_f}\mathrm E^q(\tilde x)$
  相当于让未来价格的分布 $\tilde x$ 服从风险中性概率，计算期望后折现得到当前价格
基本定理
- 第一资产定价基本定理: 资产市场中不存在套利机会，当且仅当存在状态价格向量
- 第二资产定价基本定理: 完备市场中如果不存在套利机会，则存在唯一的状态价格向量