消费者
预算约束
预算线的定义
- 多种商品的预算约束
p_1x_1+\cdots p_nx_n\le M - 两种商品的预算约束
- 令y=p_2x_2+\cdots p_nx_n,则
p_1x_1+y\le M - 或令py=p_2x_2+\cdots p_nx_n,则
p_1x_1+py\le M - 将其他商品看成复合商品y,要求p_2,\cdots,p_n同比例变动
- 令y=p_2x_2+\cdots p_nx_n,则
- 预算线和预算集
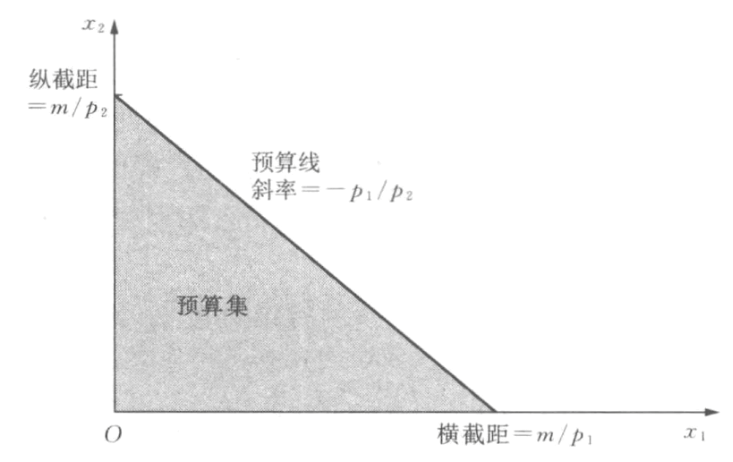
- 等号成立时: p_1x_1+p_2x_2= M
- 截距的意义: 表示单独购买一种商品的最大数量.
- 斜率的意义: 商品1增加一单位时商品2必须减少的单位数
预算线的变动
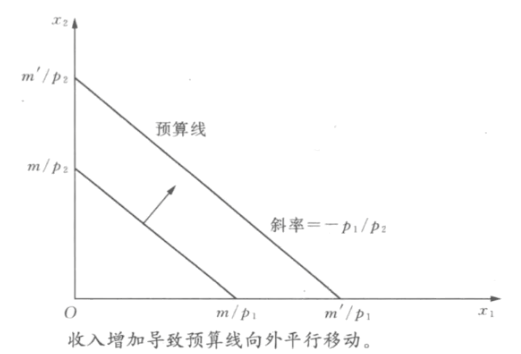
- 收入M变动
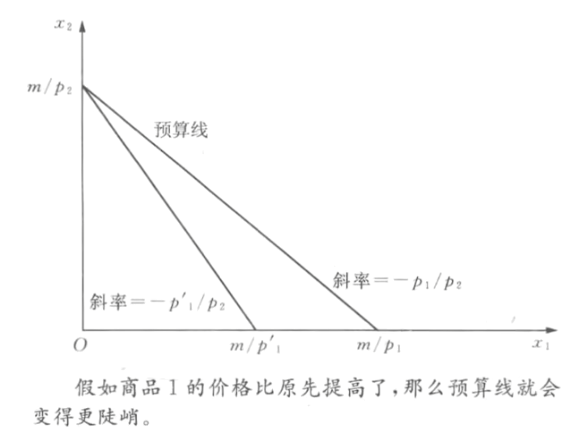
- 商品1价格p_1变动
- 价格同比例变动: 类似收入变动,预算线平移
- 税收、补贴
- 价格税与价格补贴: p_1x_1+p_2x_2= M\Rightarrow p_1(1\pm t)x_1+p_2x_2= M
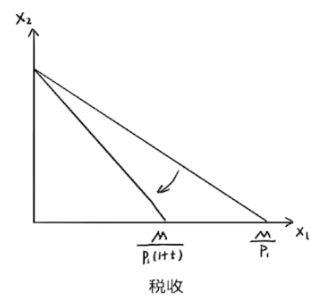
- 数量税与数量补贴: p_1x_1+p_2x_2= M\Rightarrow (p_1\pm t)x_1+p_2x_2= M
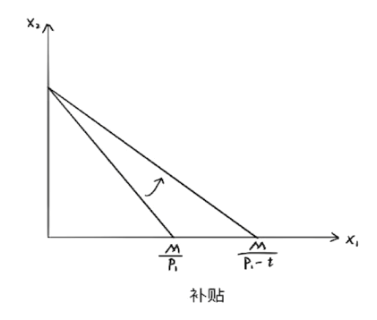
- 价格税与价格补贴: p_1x_1+p_2x_2= M\Rightarrow p_1(1\pm t)x_1+p_2x_2= M
- 配给
- 商品1存在数量上限
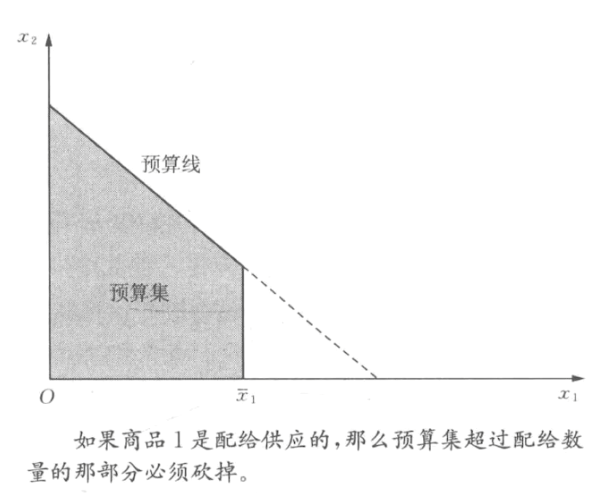
- 商品1超额配给交税(设超额价格变为p_1+t)
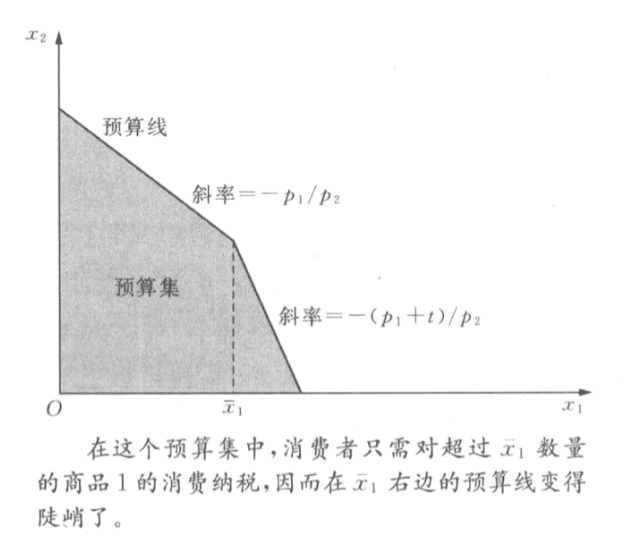
- 商品1存在数量上限
- 食品券
- 免费食品券(设面额为200)
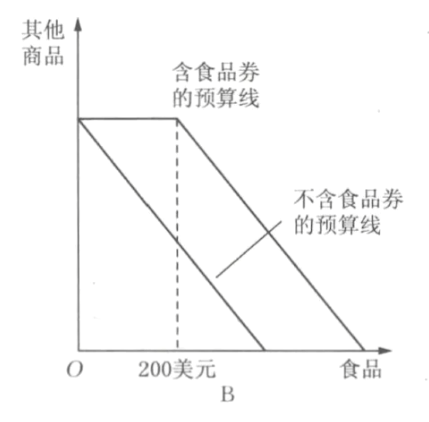
- 食品打折券(设83元可以买153元食品)
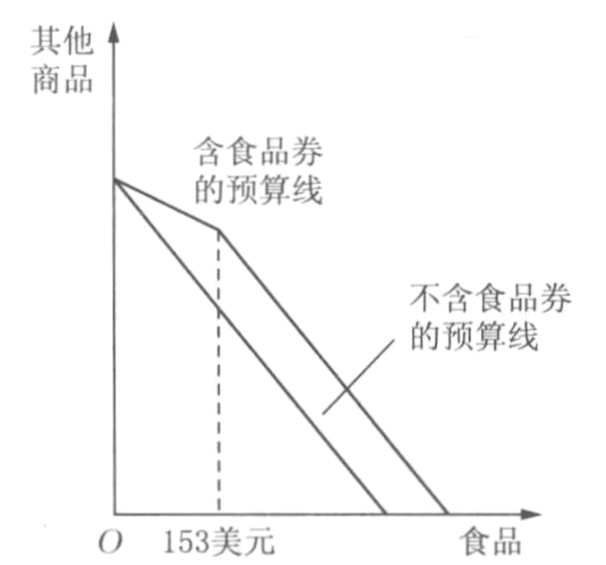
最终可以多购买70元食品
- 免费食品券(设面额为200)
偏好
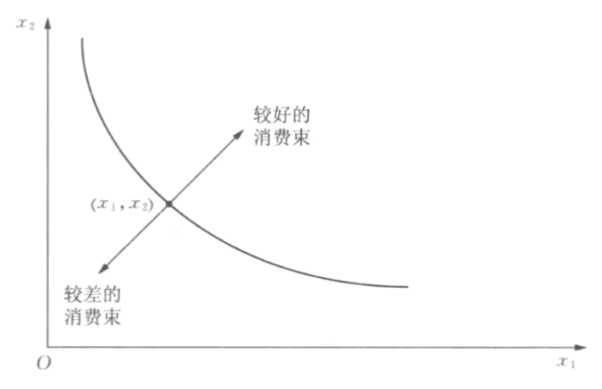
偏好的定义
- 消费束
- 消费品的组合,记为(x_1,x_2),简记为\mathbf X
- 偏好
- 消费者对不同消费束的满意程度
- \mathbf X \sim \mathbf Y: 表示消费者对\mathbf X,\mathbf Y一样满意,也称\mathbf X,\mathbf Y无差异
- \mathbf X \succ \mathbf Y: 表示消费者更喜欢\mathbf X,也称\mathbf X严格偏好于\mathbf Y
- \mathbf X \succsim \mathbf Y: 表示\mathbf X \succ \mathbf Y或\mathbf X \sim \mathbf Y,也称\mathbf X弱偏好于\mathbf Y
偏好3+3公理
- 理性人假设
- 完备性: \mathbf X \succsim \mathbf Y和\mathbf Y \succsim \mathbf X至少有一个成立
即要求消费束之间必须可比较 - 反身性: \mathbf X \succsim \mathbf X
可以得到\mathbf X \sim \mathbf X,确保行为一致 - 传递性: \mathbf X \succsim \mathbf Y\succsim \mathbf Z\rightarrow \mathbf X \succsim \mathbf Z
- 完备性: \mathbf X \succsim \mathbf Y和\mathbf Y \succsim \mathbf X至少有一个成立
- 良态偏好假设
- 连续性: \{\mathbf X\mid\mathbf X\succ \mathbf A\}下边界收敛于无差异曲线; \{\mathbf X\mid\mathbf X\prec \mathbf A\}上边界收敛于无差异曲线
避免虚线的无差异曲线 - 单调性: 若x_1\ge y_1,\cdots x_n\ge y_n且\mathbf X\ne\mathbf Y,则\mathbf X \succ\mathbf Y
避免了无差异区域,且使得无差异曲线向右下倾斜 - 凸性: 记无差异曲线A=\{(x_1,x_2)\mid(x_1,x_2)\sim(a,b)\},则\forall \mathbf X,\mathbf Y\in A,t\mathbf X+(1-t)\mathbf Y\succ A,t\in(0,1)
使得无差异曲线凸向原点
- 连续性: \{\mathbf X\mid\mathbf X\succ \mathbf A\}下边界收敛于无差异曲线; \{\mathbf X\mid\mathbf X\prec \mathbf A\}上边界收敛于无差异曲线
- 良态无差异曲线
偏好实例
- 完全替代品
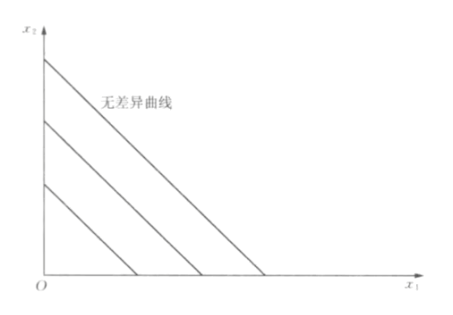
- 消费者按照固定比例使用一种商品替代另一种商品.
- 完全互补品
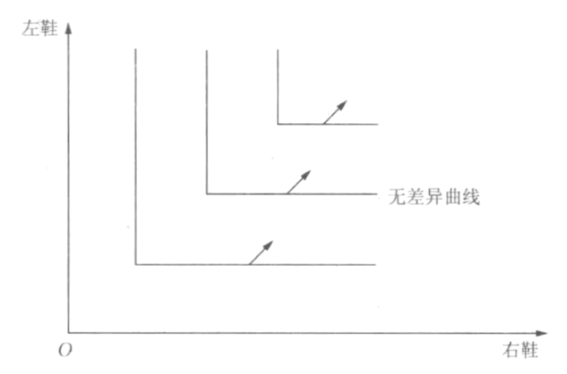
- 必须按照固定比例搭配使用的商品.
- 厌恶品
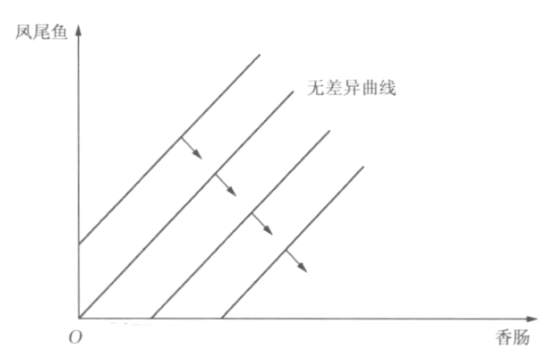
- 消费者不喜欢的商品,只会带来厌恶感
- 中性商品
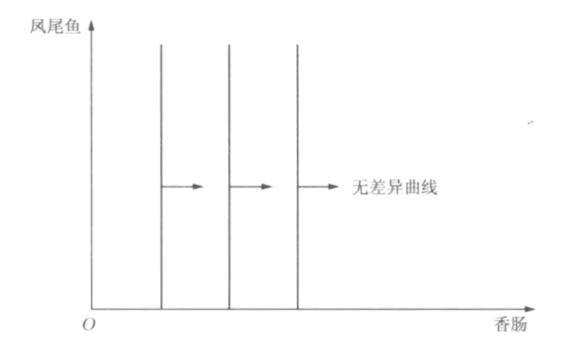
- 消费者不在乎的商品
- 餍足
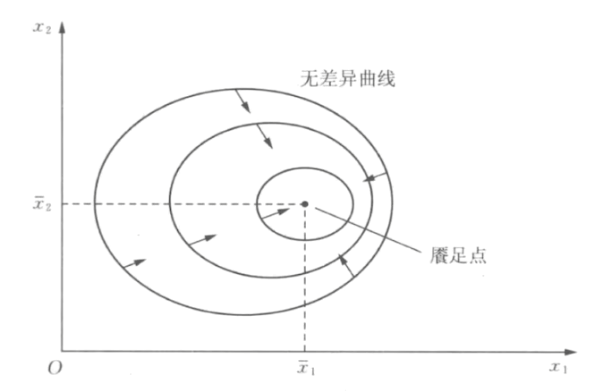
- 消费束越某个点,消费者越满意
边际替代率
- 定义
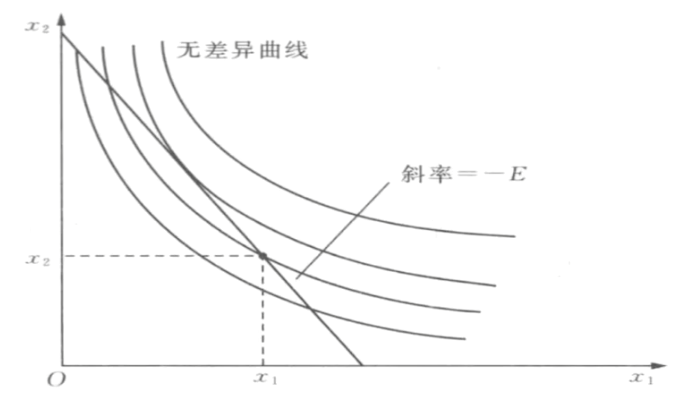
- 无差异曲线的斜率,记为MRS
- MRS_{12}=\frac{\Delta x_2}{\Delta x_1}=\frac{\mathrm dx_2}{\mathrm d x_1}
- 作用
- 增加1单位商品1,减少MRS单位商品2时效用不变
- 当MRS与预算线斜率不等时,消费者有动机继续交换商品
效用
效用简介
- 从偏好到效用
- 效用是描述和实现偏好的一种方式

- 存在无数种指派方式,都能够正确的反映偏好关系。将指派的数值称作效用,将指派方式称作效用函数
- 效用是描述和实现偏好的一种方式
- 基数效用与序数效用
- 基数效用理论: 效用的绝对值是有意义的,反映满足程度,可以用来加总
- 序数效用理论: 效用的绝对值没有意义,不能加总,只能进行排序
边际效用
- 表示增加一单位商品带来的效用,对于效用函数u=u(x_1,x_2)
- MU_1=\frac{\partial u}{\partial x_1}=u_1^\prime
- MU_2=\frac{\partial u}{\partial x_2}=u_2^\prime
- 货币的边际效用
- 假设商品价格为p_1,p_2,则一单位货币的边际效用为\frac{MU_1}{p_1},\frac{MU_2}{p_2}
- 边际效用的性质
- 边际效用递减: \frac{\partial MU_1}{\partial x_1}=u_{11}^{\prime\prime}\lt0
- 货币边际效用不变: \frac{MU_1}{p_1}=\frac{MU_2}{p_2}=\lambda
- 边际效用与边际替代率
- 计算边际替代率: MRS_{12}=-\frac{MU_1}{MU_2}
- 正单调变换不改变边际替代率: MRS_{12}=-\frac{f^\prime u_1^\prime}{f^\prime u_2^\prime}=-\frac{u_1^\prime}{ u_2^\prime}=-\frac{MU_1}{MU_2}
- 边际效用递减与边际替代率递减完全没有推导关系
效用函数
- 完全替代的效用函数: u=ax_1+bx_2
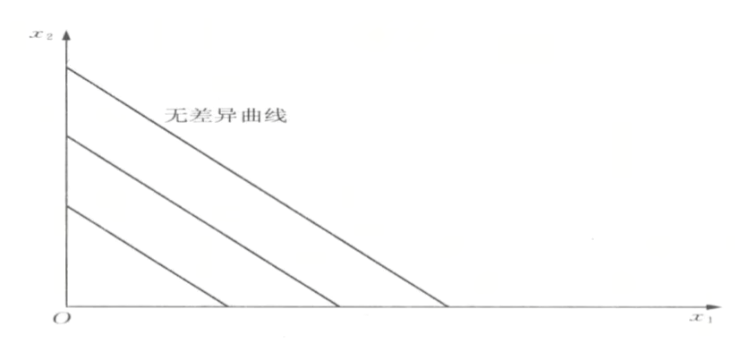
- 表示b个商品1与a个商品2的效用相同
- 完全互补的效用函数: u=\min (ax_1,bx_2)
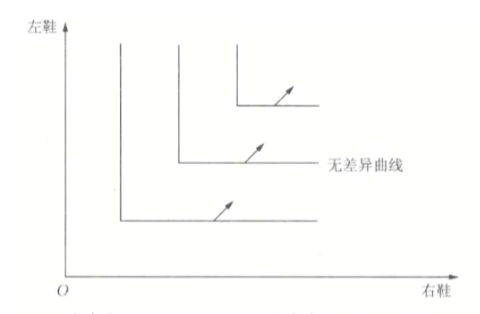
- 表示b个商品1必须搭配a个商品2使用
- 拟线性效用函数: u=v(x_1)+x_2,v^{\prime\prime}(x)\lt0
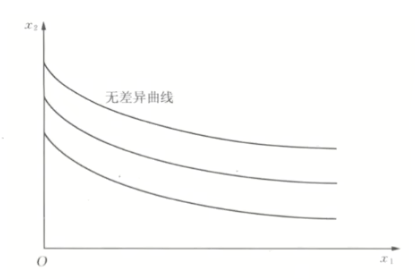
- 可以沿x_2平移得到新的无差异曲线,移动一单位后效用也变动一单位
- 对于不同效用下的无差异曲线,x_1相同时斜率都相同
- 柯布道格拉斯效用: u=x_1^cx_2^d
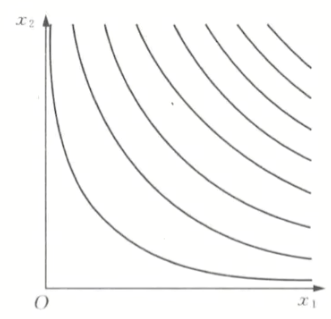
- 对数变换: v=\ln u=c\ln x_1+d\ln x_2
- 幂变换: v=u^{\frac{1}{c+d}}=x_1^{\frac{c}{c+d}}x_2^{\frac{d}{c+d}}=x_1^ax_2^{1-a}
选择
图像法
- 良态
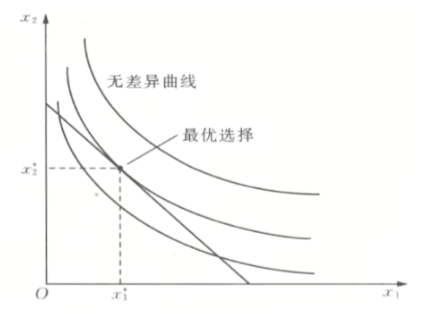
- 折拗的偏好
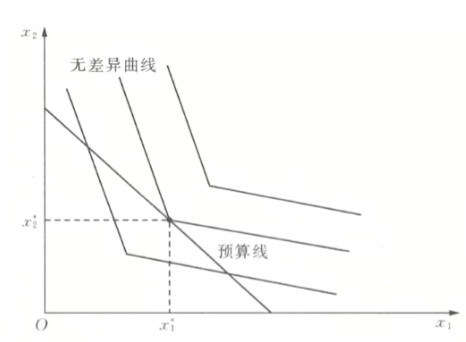
- 角点解
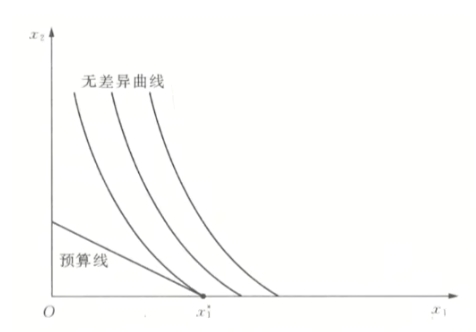
- 非良态
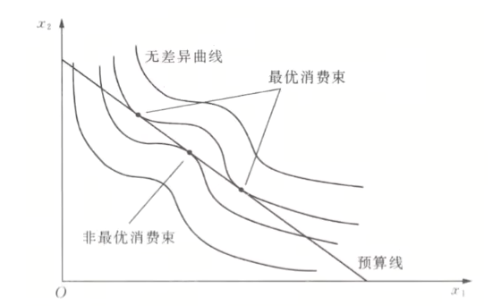
代数法
- 代入法
\max u(x_1,x_2)\Rightarrow \max u\left(x_1,\frac{M-p_1x_1}{p_2} \right)\Rightarrow u_1^\prime-\frac{p_1}{p_2}u^\prime_2=0 - 拉格朗日乘数法
\begin{align} &L=u-\lambda(p_1x_1+p_2x_2-M) \\ &\begin{cases} &\frac{\partial L}{\partial x_1}=u_1^\prime-\lambda p_1=0 \\ &\frac{\partial L}{\partial x_2}=u_2^\prime-\lambda p_2=0 \\ &\frac{\partial L}{\partial \lambda}=M-p_1x_1+p_2x_2=0 \end{cases} \end{align} - 柯布道格拉斯偏好
\begin{align} &x_1^\ast=\frac{c}{c+d}\frac{M}{p_1} \\ &x_2^\ast=\frac{d}{c+d}\frac{M}{p_2} \end{align}
马歇尔需求
需求变动因素
- 通过求解效用最大化问题,得到x_1=x_1(p_1,p_2,M),称为马歇尔需求
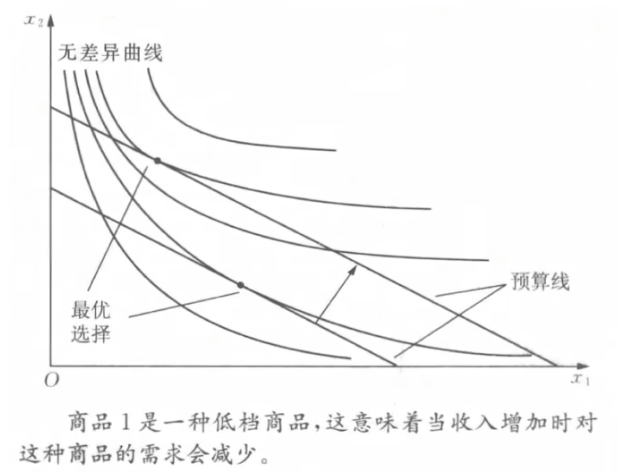
- 正常商品与低档商品
- 正常商品: \frac{\partial x_1}{\partial M}\gt 0
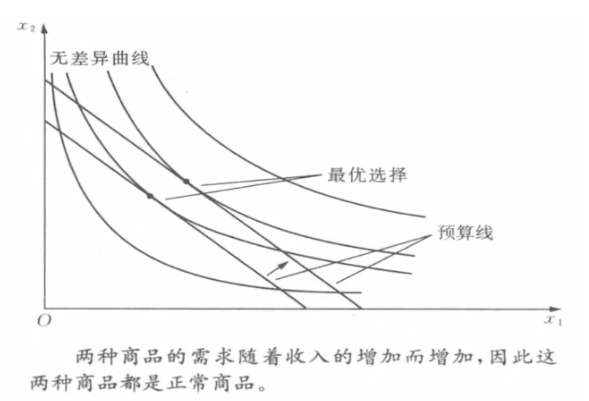
- 低档商品: \frac{\partial x_1}{\partial M}\lt 0
- 正常商品: \frac{\partial x_1}{\partial M}\gt 0
- 奢侈品与必需品
- 奢侈品: \frac{\partial \ln x_1}{\partial \ln M}\gt 1
与收入增加的比例相比,需求增加的比例更大 - 必需品: \frac{\partial \ln x_1}{\partial \ln M}\lt 1
与收入增加的比例相比,需求增加的比例更小
- 奢侈品: \frac{\partial \ln x_1}{\partial \ln M}\gt 1
- 普通商品与吉芬商品
- 普通商品: \frac{\partial x_1}{\partial p_1}\lt 0
价格上升,需求下降 - 吉芬商品: \frac{\partial x_1}{\partial p_1}\gt 0
价格上升,需求增加
- 普通商品: \frac{\partial x_1}{\partial p_1}\lt 0
- 替代与互补
- 替代: \frac{\partial x_1}{\partial p_2}\gt 0
商品二价格上升,商品二数量下降,但是商品一数量上升 - 互补: \frac{\partial x_1}{\partial p_2}\lt 0
商品二价格上升,商品二数量下降,商品一数量也下降
- 替代: \frac{\partial x_1}{\partial p_2}\gt 0
需求-收入曲线
- 收入提供曲线
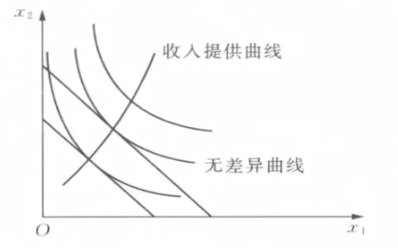
- 展示了两种商品x_1,x_2对收入M变化的反应
- x_1=x_1(p_1,p_2,M),x_2=x_2(p_1,p_2,M)\Rightarrow f(x_1,x_2,p_1,p_2)=0
- 恩格尔曲线
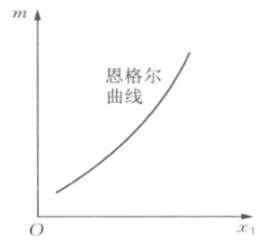
- 展示了一种商品x_1与收入M的关系
- x_1=x_1(p_1,p_2,M)\Rightarrow f(x_1,M)=0
- 几个实例
- 完全替代
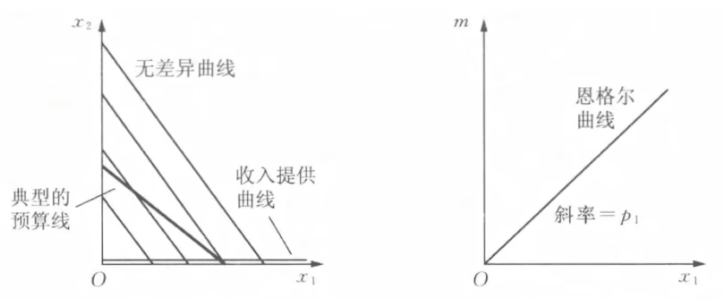
- 完全互补
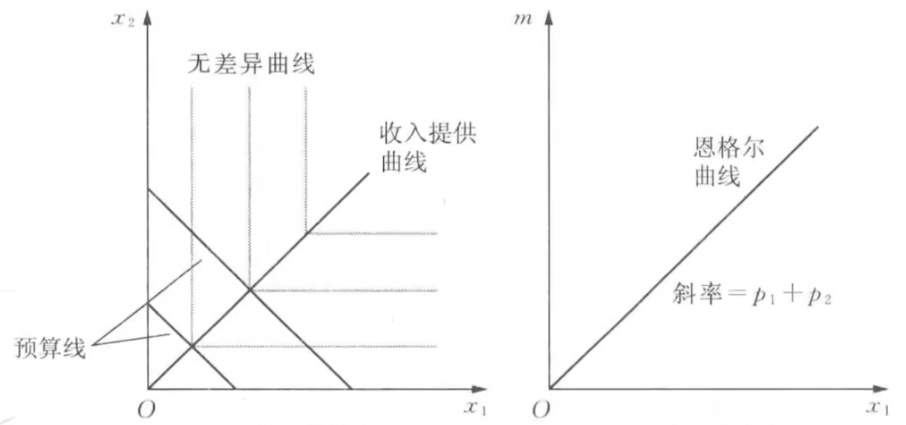
- 柯布道格拉斯
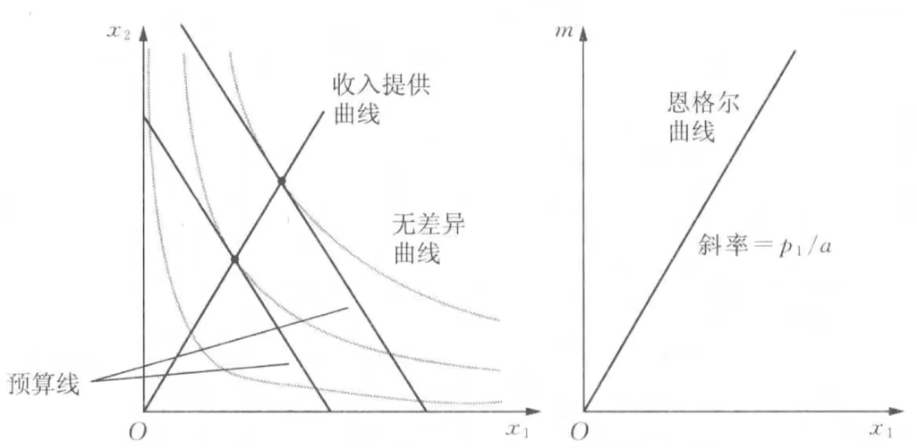
- 拟线性偏好
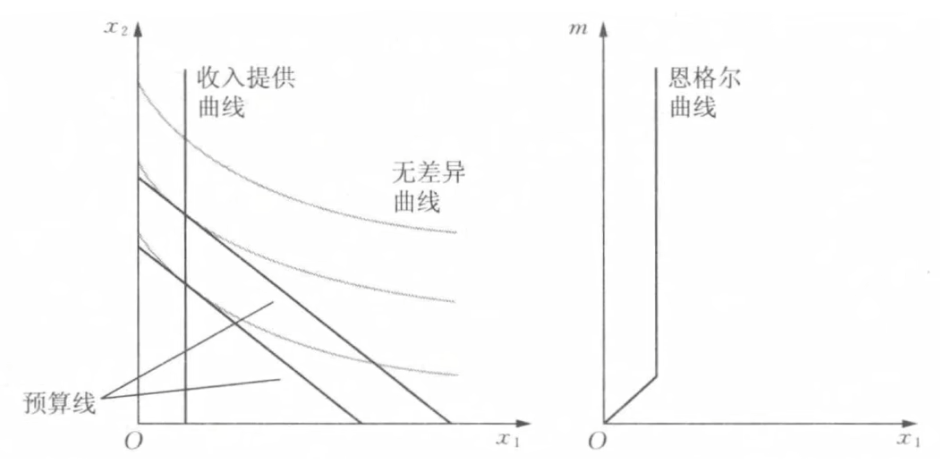
- 完全替代
- 相似偏好(位似偏好)
- 相似偏好: 收入提供曲线和恩格尔曲线均是直线(假设价格不变)
- 完全互补偏好: 消费者总是按与价格无关的特定比例消耗两种商品
需求-价格曲线
- 价格提供曲线
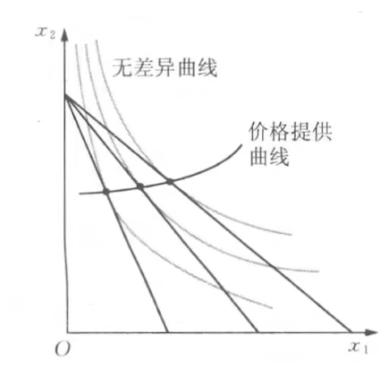
- 展示了两种商品x_1,x_2与价格p_1的关系
- x_1=x_1(p_1,p_2,M),x_2=x_2(p_1,p_2,M)\Rightarrow f(x_1,x_2,p_2,M)=0
- 需求曲线
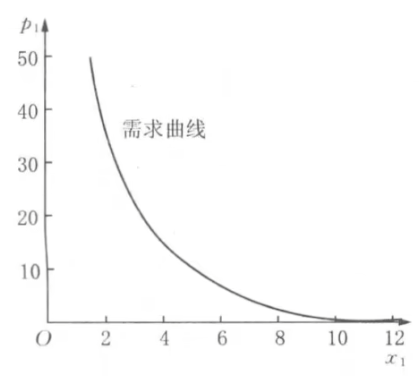
- 展示了一种商品x_1与价格p_1的关系
- x_1=x_1(p_1,p_2,M)\Rightarrow f(x_1,p_1)=0
- 几个实例
- 完全替代
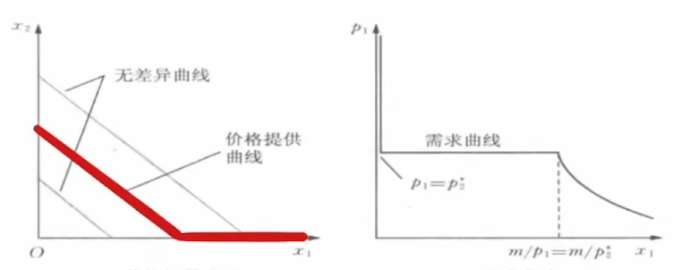
- 完全互补
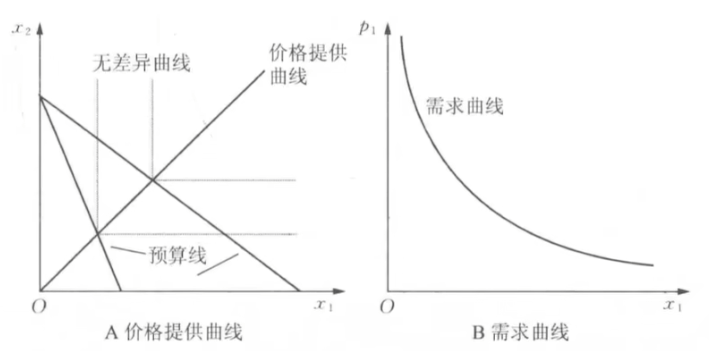
- 完全替代
反需求函数
- 把需求曲线看作是作为数量的函数的价格的测度,你就得到一个反需求函数.
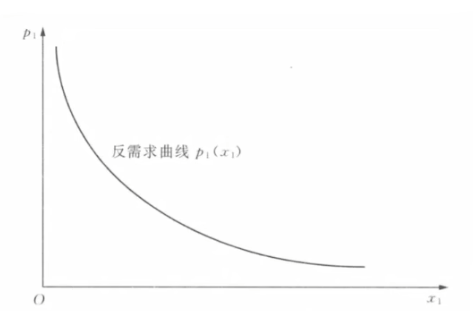
- x_1=x_1(p_1,p_2,M)\Rightarrow p_1=p_1(x_1)
- 边际支付意递减
- 当商品一的数量较少时,我们愿意放弃很多其他商品支出,来换取一单位商品一
- 当商品一的数量很大时,我们只愿意放弃较少的其他商品支出,来换取一单位商品一
斯勒茨基方程
替代与收入效应
- 替代效应
- 商品一价格变化后,保持购买力不变,商品二与商品一的替代关系
- 收入效应
- 价格变化后,带来的相对收入的增加,会导致商品需求的变化
斯勒茨基分解
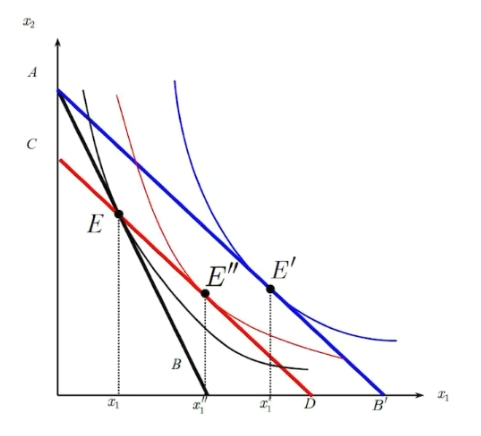
- 假设E^{\prime\prime}过原消费束
- 此时\Delta M=\Delta p_1x_1
- 替代效应
\Delta x_1^s=E^{\prime\prime}-E=x_1(p_1+\Delta p_1,M+\Delta p_1x_1)-x_1(p_1,M) - 收入效应
\Delta x_1^m=E^{\prime}-E^{\prime\prime}=x_1(p_1+\Delta p_1,M)-x_1(p_1+\Delta p_1,M+\Delta p_1x_1) - 分解
\Delta x_1=\Delta x_1^s+\Delta x_1^m\Rightarrow \frac{\partial x_1}{\partial p_1}=\frac{\partial x_1^s}{\partial p_1}-\frac{\partial x_1^m}{\partial M}x_1 - 分析
- \frac{\partial x_1^s}{\partial p_1}总是小于等于0; \frac{\partial x_1^m}{\partial M}符号不确定
- 正常商品: \frac{\partial x_1^m}{\partial M}\gt 0,此时\frac{\partial x_1}{\partial p_1}\lt 0,即一定为普通商品
- 低档商品: \frac{\partial x_1^m}{\partial M}\lt 0。若\frac{\partial x_1^m}{\partial M}足够小则\frac{\partial x_1}{\partial p_1}\gt 0,此时为吉芬商品
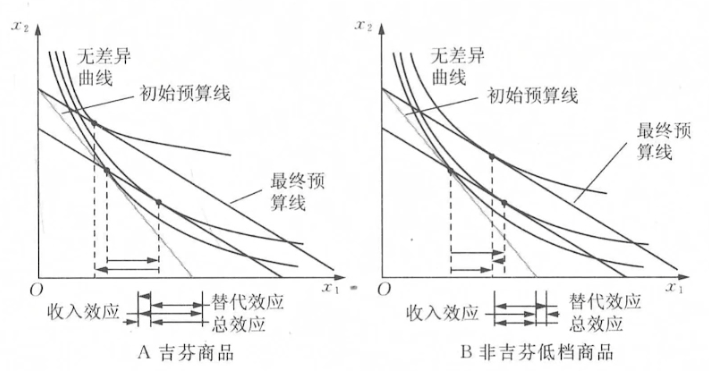
- 实例
- 完全互补: 只有收入效应
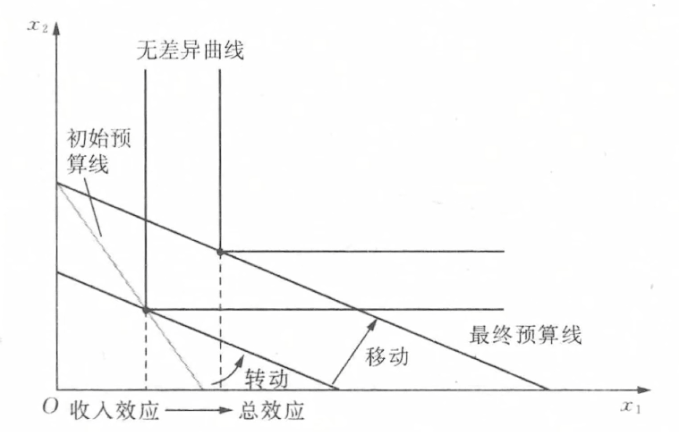
- 完全替代: 只有替代效应
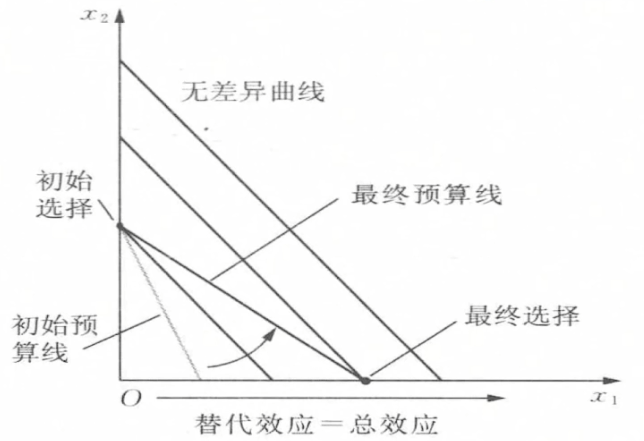
- 拟线性偏好: 只有替代效应
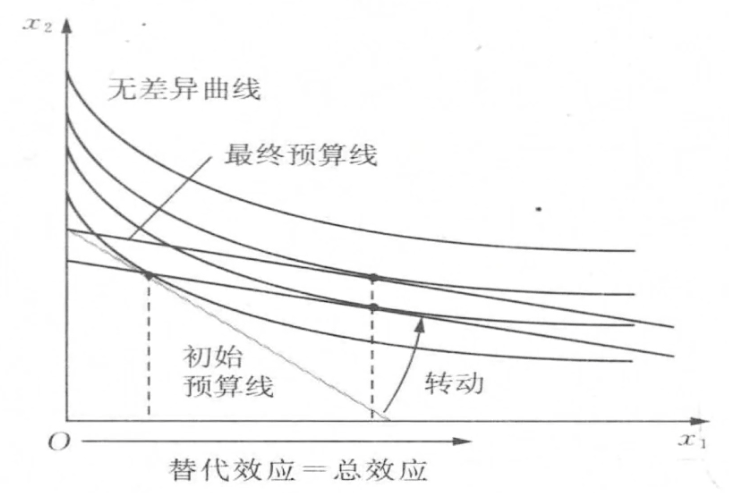
- 完全互补: 只有收入效应
希克斯分解
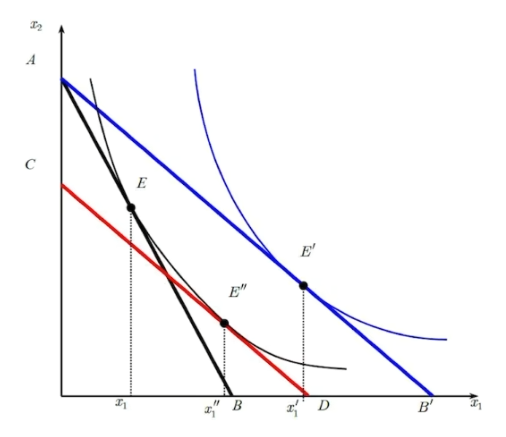
- 假设E^{\prime\prime}与原效用函数相切
- 希格斯函数h_1(p_1,p_2,\bar u): 给定效用水平与效用函数\bar u=u(x_1,x_2)使得p_1x_1+p_2x_2最小时的x_1
- 支出函数e(p_1,p_2,\bar u): 给定效用水平与效用函数\bar u=u(x_1,x_2)使得p_1x_1+p_2x_2最小时的支出M
- 间接效用函数v(p_1,p_2,M): 给定效用函数u(x_1,x_2)和预算约束线p_1x_1+p_2x_2时的最大效用\bar u
- 分解
\frac{\partial x_1(p_1,p_2,M)}{\partial p_1}=\frac{\partial h_1(p_1,p_2,v(p_1,p_2,M))}{\partial p_1}-\frac{\partial x_1(p_1,p_2,M)}{\partial M}x_1(p_1,p_2,M) - 分析
- \frac{\partial h_1}{\partial p_1}总是小于等于0; \frac{\partial x_1}{\partial M}符号不确定
显示偏好
显示偏好概念
- 预算集
- 将\{(x_1,x_2)\mid p_1x_1+p_2x_2\le M\}记为\mathcal{B} (p_1,p_2,M)
- 显示偏好的假设
- 挥霍性: 消费者总是花光所有收入。这保证了消费者在预算线上进行选择
- 唯一性: 消费者的最终选择是唯一的。保证了选择的唯一性
- 差异性: 给定不同的预算集\mathcal{B}_1和\mathcal{B}_2,相应的最终选择为\mathbf X_1和\mathbf X_2,则\mathbf X_1\ne\mathbf X_2
- 显示偏好的定义
- 若\mathbf X_1,\mathbf X_2\in\mathcal{B},消费者最终选择了\mathbf X_1,则称\mathbf X_1被直接显示偏好于\mathbf X_2
- 显示偏好的性质
- 由于挥霍性,而又选择了\mathbf X_1,因此一定有\mathbf P\mathbf X_1=M
- 由于\mathbf X_2\in \mathcal{B},因此\mathbf P\mathbf X_1=M\ge \mathbf P\mathbf X_2
显示偏好弱公理
- 显示偏好弱公理的内容
- 若\mathbf X_1被直接显示偏好于\mathbf X_2,且\mathbf X_1\ne\mathbf X_2,则\mathbf X_2被直接显示偏好于\mathbf X_1不成立
- 若成立,则有\mathbf P_1\mathbf X_1\ge \mathbf P_1\mathbf X_2,\mathbf P_2\mathbf X_1\le \mathbf P_2\mathbf X_2,有以下反例
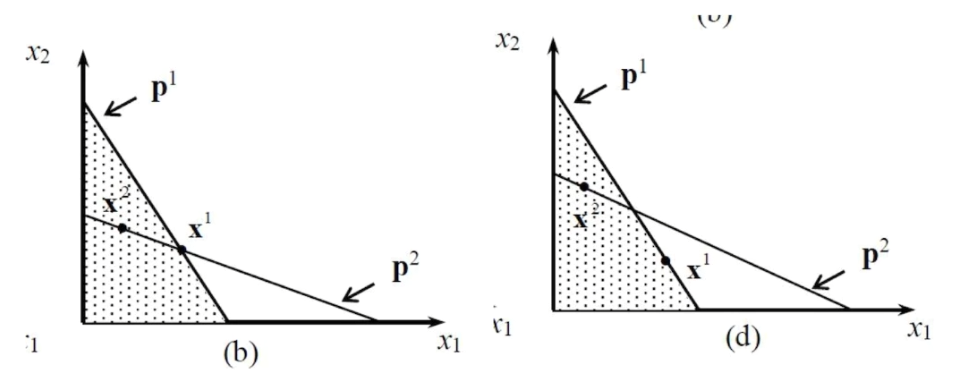
- \mathbf X_1,\mathbf X_2\in \mathcal{B_1}\cap \mathcal{B_2},对同一个预算集\mathcal{B_1}\cap \mathcal{B_2}两次却有不同选择,因此矛盾
- 显示偏好弱公理的检验检验
- 绘制矩阵(\mathbf P_1,\mathbf P_2,\mathbf P_3)^\top(\mathbf X_1,\mathbf X_2,\mathbf X_3)
\begin{bmatrix} \mathbf P_1\mathbf X_1 & \mathbf P_1\mathbf X_2 & \mathbf P_1\mathbf X_3\\ \mathbf P_2\mathbf X_1 & \mathbf P_2\mathbf X_2 & \mathbf P_2\mathbf X_3\\ \mathbf P_3\mathbf X_1 & \mathbf P_3\mathbf X_2 & \mathbf P_3\mathbf X_3 \end{bmatrix} - 一行行比较主对角线元素和非对角线元素,若非对角线元素小于该行对角线元素则标记星号
\begin{bmatrix} 5 & 4^\ast & 6\\ 4^\ast & 5 & 6\\ 3^\ast & 3^\ast & 4 \end{bmatrix} - 若存在关于主对角线对称的星号,则违反显示偏好弱公理
- 绘制矩阵(\mathbf P_1,\mathbf P_2,\mathbf P_3)^\top(\mathbf X_1,\mathbf X_2,\mathbf X_3)
显示偏好强公理
- 间接显示偏好
- 若\mathbf X_1被直接显示偏好于\mathbf X_2,\mathbf X_2被直接显示偏好于\mathbf X_3,则\mathbf X_1被间接显示偏好于\mathbf X_3
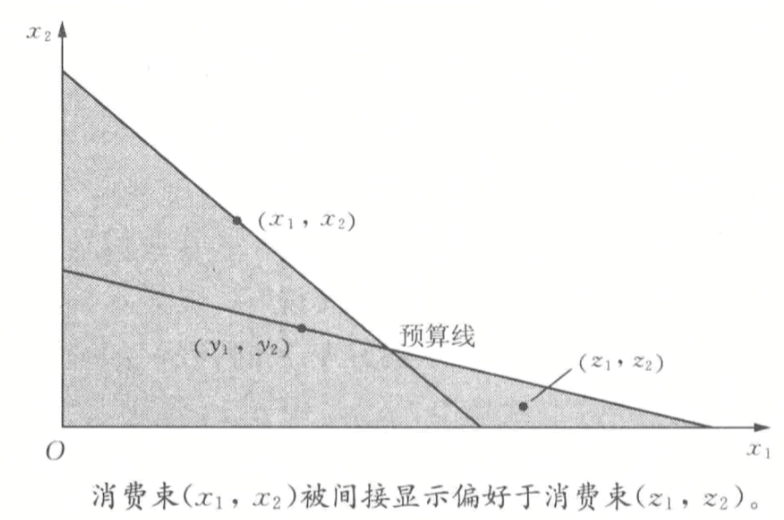
- 若\mathbf X_1被直接显示偏好于\mathbf X_2,\mathbf X_2被直接显示偏好于\mathbf X_3,则\mathbf X_1被间接显示偏好于\mathbf X_3
- 显示偏好原理
- 假设消费者按照偏好六公理行事,若\mathbf X_1被直接或间接显示偏好于\mathbf X_2,则\mathbf X_1\succ \mathbf X_2
- 显示偏好强公理的内容
- 若\mathbf X_1被直接或间接显示偏好于\mathbf X_2,且\mathbf X_1\ne\mathbf X_2,则\mathbf X_2被直接或间接显示偏好于\mathbf X_1不成立
- 可由显示偏好原理推导而来
- 显示偏好强公理的检验
- 用检验弱公理的方法绘制矩阵
- 根据直接显示偏好,找到所有间接显示偏好,标记为(*)
- 若(*)或*关于主对角线对称,则违反显示偏好强公理
指数
- 帕氏指数
- 数量指数
P=\frac{\sum p^tx^t}{\sum p^tx^0}
若P\gt1则t期消费束被直接显示偏好于0期消费束 - 价格指数
P=\frac{\sum p^tx^t}{\sum p^0x^t}
- 数量指数
- 拉氏指数
- 数量指数
L=\frac{\sum p^0x^t}{\sum p^0x^0}
若L\lt1则0期消费束被直接显示偏好于t期消费束 - 价格指数
L=\frac{\sum p^tx^0}{\sum p^0x^0}
- 数量指数
购买与销售
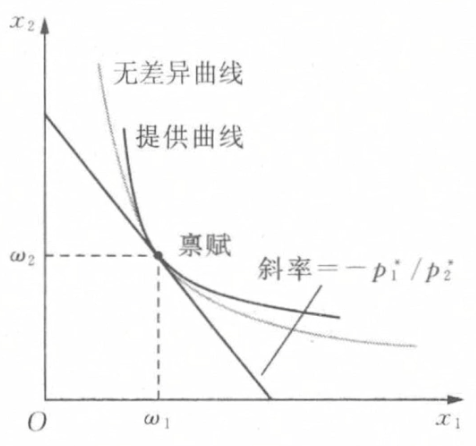
禀赋
- 禀赋的定义
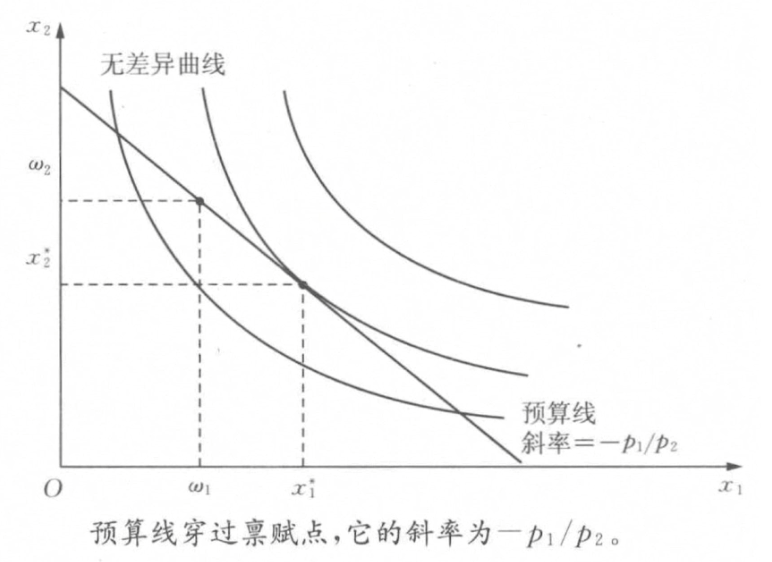
- 假设初始拥有商品束(\omega_1,\omega_2)(又称为禀赋),则M变为p_1\omega_1+p_2\omega_2
- 对于禀赋束,人们一定选择\mathbf P\mathbf \Omega最大的;对于消费束不一定选择\mathbf P\mathbf X最大的,而是看谁效用更大
- 扩展的预算约束
p_1x_1+p_2x_2=p_1\omega_1+p_2\omega_2\Rightarrow p_1(x_1-\omega_1)+p_2(x_2-\omega_2)=0
- 禀赋变动
- 数量变动: 影响收入,但是斜率不变
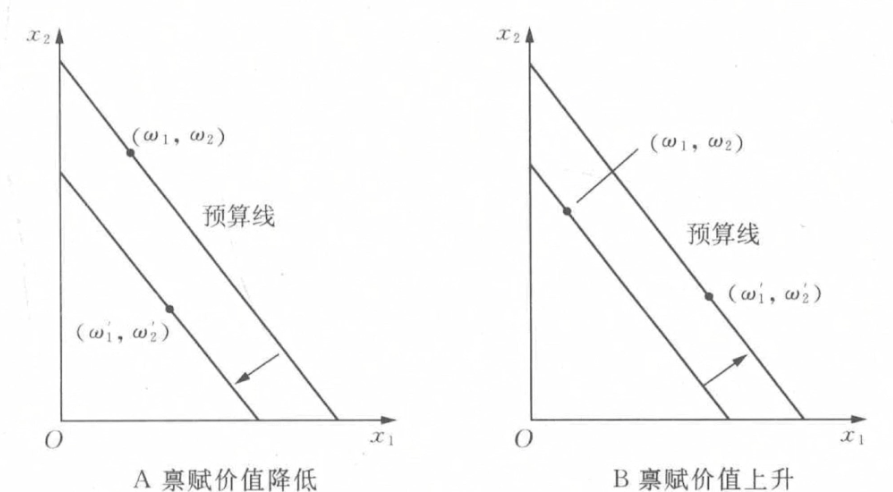
- 价格变动: 影响斜率,但过原禀赋点
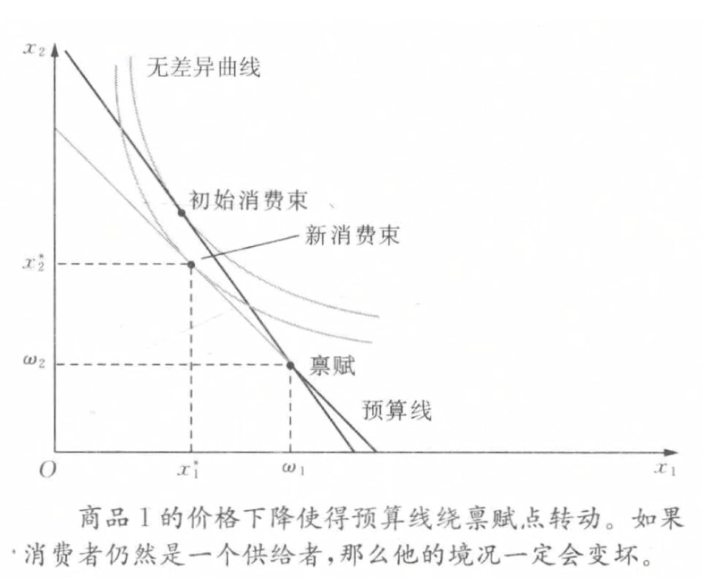
消费者是商品一的净供给者,商品一价格下降,若消费者依然选择成为给净供给者,则消费者境况必然变坏
消费者是商品一的净供给者,商品一价格上升,则消费者依然选择成为给净供给者,且消费者境况必然变好
消费者是商品一的净购买者,商品一价格上升,若消费者依然选择成为给净购买者,则消费者境况必然变坏
消费者是商品一的净购买者,商品一价格下降,则消费者依然选择成为给净购买者,且消费者境况必然变好
- 数量变动: 影响收入,但是斜率不变
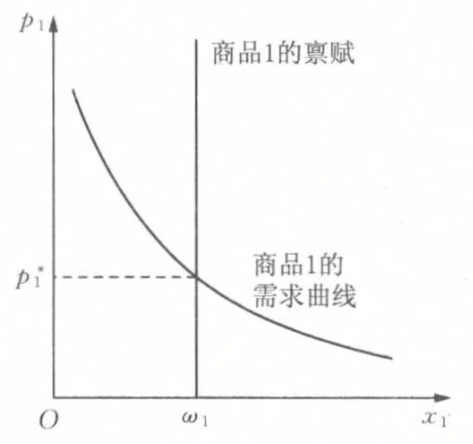
- 提供曲线和需求曲线
- 提供曲线: 价格p_1变动时的(x_1,x_2)
- 需求曲线: 价格p_1变动时的x_1
- 总需求、净需求和净供给
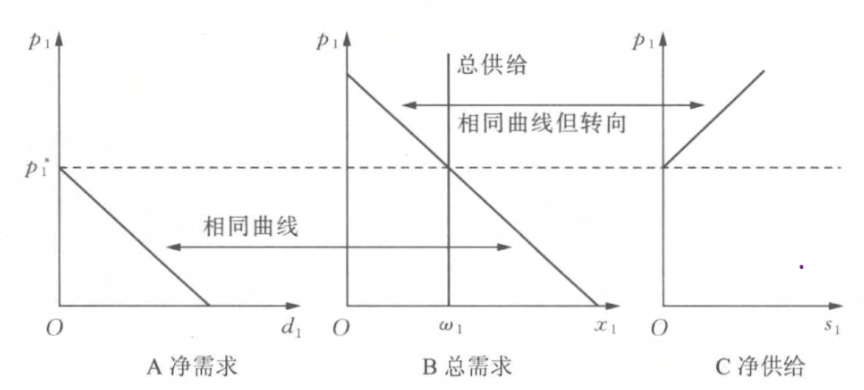
- 提供曲线: 价格p_1变动时的(x_1,x_2)
修正的斯勒茨基方程
- 公式
\frac{\mathrm d x_1(p_1,p_2,M)}{\mathrm d p_1}=\frac{\partial x_1^s}{\partial p_1}+\frac{\partial x_1^m}{\partial M}(\omega_1-x_1)=\frac{\partial x_1^s}{\partial p_1}-\frac{\partial x_1^m}{\partial M}x_1+\frac{\partial x_1^m}{\partial M}\omega_1 - 需求的总变动 = 替代效应引起的变动 + 普通收入效应引起的需求变动 + 禀赋收入效应引起的需求变动
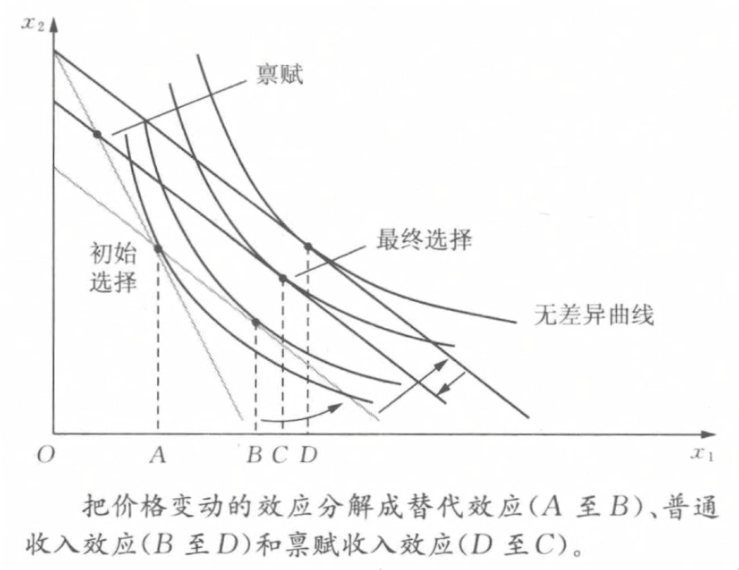
劳动供给
- 公式
pC=p\bar C+\omega(\bar R-R)\Rightarrow pC+\omega R=p\bar C+\omega\bar R- \omega: 工资率
- \bar C: 禀赋
- C: 消费
- \bar R: 一天的时间
- R: 休息的时间
- 最优化
\max_{C,R}u(C,R)\quad \mathrm{s.t.}\quad pC+\omega R=p\bar C+\omega\bar R- 最终条件: MRS=-\frac{\omega}{p}
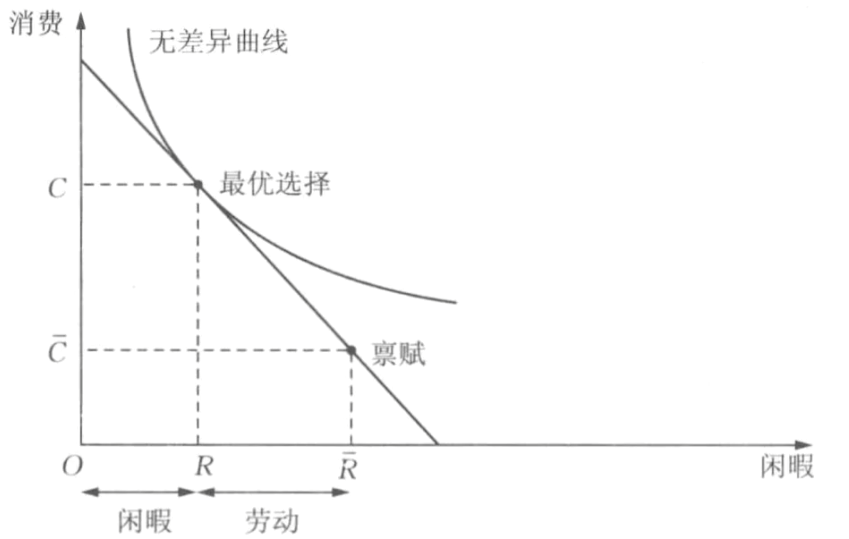
- 最终条件: MRS=-\frac{\omega}{p}
- 比较静态分析
\frac{\partial R}{\partial \omega}=\frac{\partial R^s}{\partial \omega}+\frac{\partial R^m}{\partial M}(\bar R- R)- 其中\frac{\partial R^s}{\partial \omega}\lt0,\frac{\partial R^m}{\partial M}\gt 0
- \omega较小时,\bar R- R小,\frac{\partial R}{\partial \omega}为负,工资增加导致劳动增加
- \omega较大时,\bar R- R大,\frac{\partial R}{\partial \omega}为正,工资增加导致劳动减少
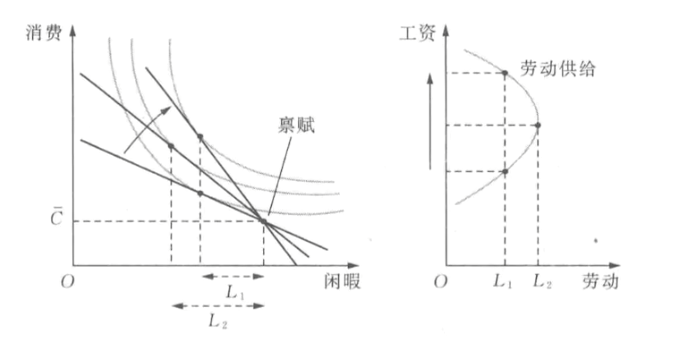
跨期选择
均衡分析
- 预算约束
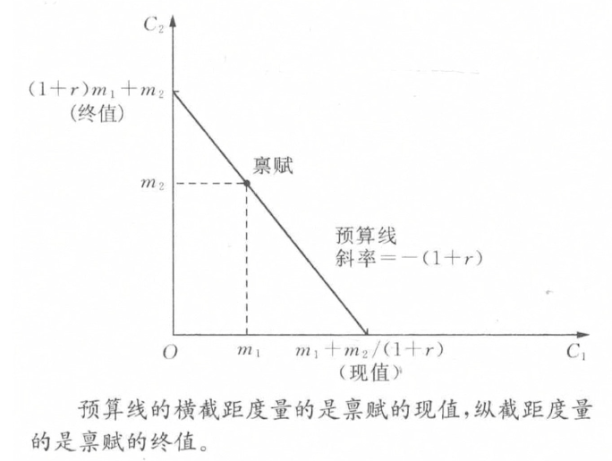 (1+r)c_1+c_2=(1+r)m_1+m_2
(1+r)c_1+c_2=(1+r)m_1+m_2
- c: 支出
- m: 收入
- 特殊情况
- 若第一期不允许借,则只有禀赋点左侧部分
- 若借贷利率r_b,r_l不同,禀赋点右侧斜率为r_b,左侧为r_l
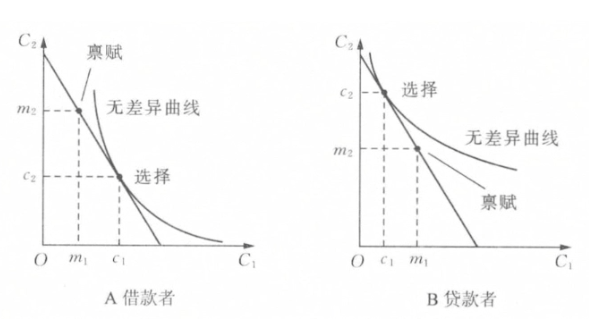
- 比较静态分析
- 消费者是贷款者,若利率上升,则消费者依然是贷款者,且境况变好
- 消费者是贷款者,若利率下降,消费者依然选择是贷款者,则境况变坏
- 消费者是借款者,若利率下降,则消费者依然是借款者,且境况变好
- 消费者是借款者,若利率上升,消费者依然选择是借款者,则境况变坏
- 斯勒茨基方程
\frac{\partial c_1}{\partial r}=\frac{\partial c_1^s}{\partial r}+\frac{\partial c_1^m}{\partial M}(m_1- c_1)- 其中\frac{\partial c_1^s}{\partial r}\lt0,\frac{\partial c_1^m}{\partial M}\gt0
- 对于借款者,m_1- c_1\lt0,因此\frac{\partial c_1}{\partial r}\lt0,利率上升减少当期消费
其他分析
- 考虑通胀
\frac{1+r}{1+\pi}c_1+c_2=\frac{1+r}{1+\pi}m_1+m_2\Rightarrow (1+\rho)c_1+c_2=(1+\rho)m_1+m_2- \rho=\frac{r-\pi}{1+\pi}\approx r-\pi
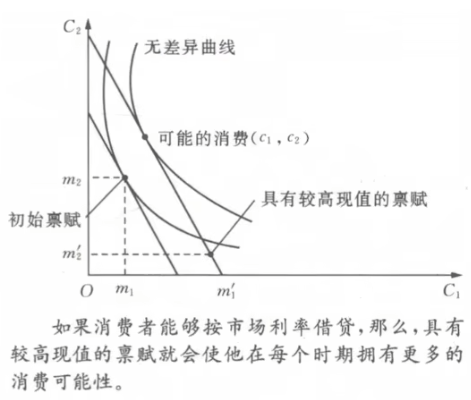
- 现值分析
- PV=m_1+\frac{m_2}{1+r}
- PV高的预算束靠外
剩余
消费者剩余
- 离散需求,假设拟线性效用u(x_1,x_2)=v(x_1)+x_2
- 总剩余: v(x_1^\ast)
- 净剩余: v(x_1^\ast)-px_1^\ast
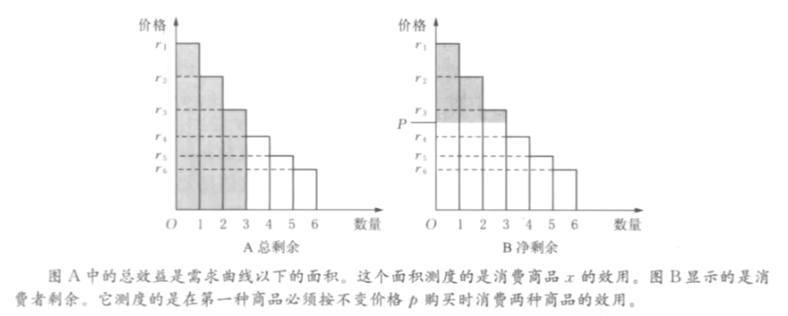
- 连续需求,总需求曲线p_1=p_1(x_1)
- 总剩余: \int_0^{x_1^\ast}p_1(x_1)\mathrm d x_1
- 净剩余: \int_0^{x_1^\ast}p_1(x_1)\mathrm d x_1-p_1(x_1^\ast)x_1^\ast
- 净剩余的变化
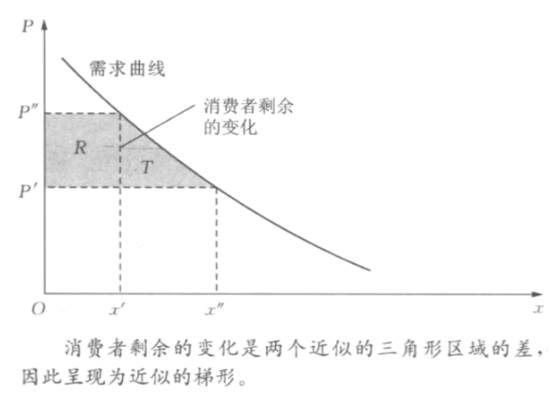 \Delta=\int_{p^{\prime}}^{p^{\prime\prime}}x_1(p_1)\mathrm d p_1
\Delta=\int_{p^{\prime}}^{p^{\prime\prime}}x_1(p_1)\mathrm d p_1
- 补偿变化与等价变化
- 假设(\mathbf P,M)情况下最大效用为U_1,价格上升后(\mathbf P^\prime,M)下最大效用为U_2
- 若价格上升后给予补偿到(\mathbf P^\prime,M+\Delta M)使得效用仍为U_1,称为收入的补偿变化
- 若价格上升前拿走收入到(\mathbf P,M-\Delta M)使得效用变为U_2,称为等价变化
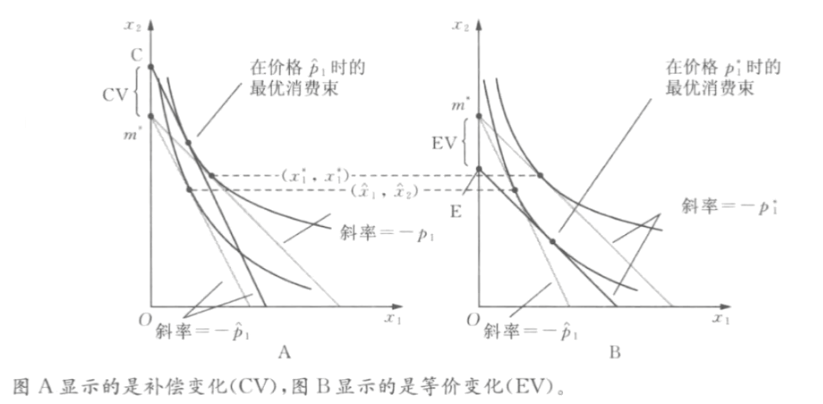
- 拟线性偏好下,等价变化和补偿变化的\Delta M相同的,均为\Delta U
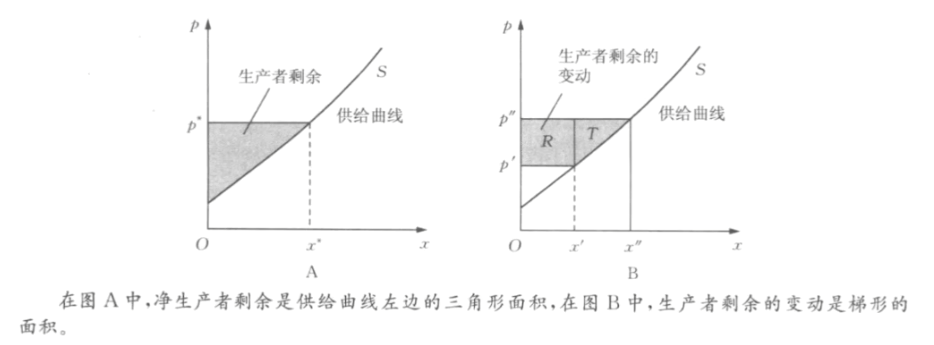
生产者剩余
- 供给曲线p=p(x)
- 增加一单位商品,供给者愿意接受的最低价格
- 生产者剩余
p(x^\ast)x^\ast-\int_0^{x^\ast}p(x)\mathrm dx
成本收益分析
市场需求
需求函数
- 简化假设,认为市场的需求函数与个人的马歇尔需求函数形式相同
X_1=X_1(p_1,p_2,M)=Q(p_1)- 需求函数: Q_d=Q(P)
- 反需求函数: P=P(Q_d)=Q^{-1}(Q_d)
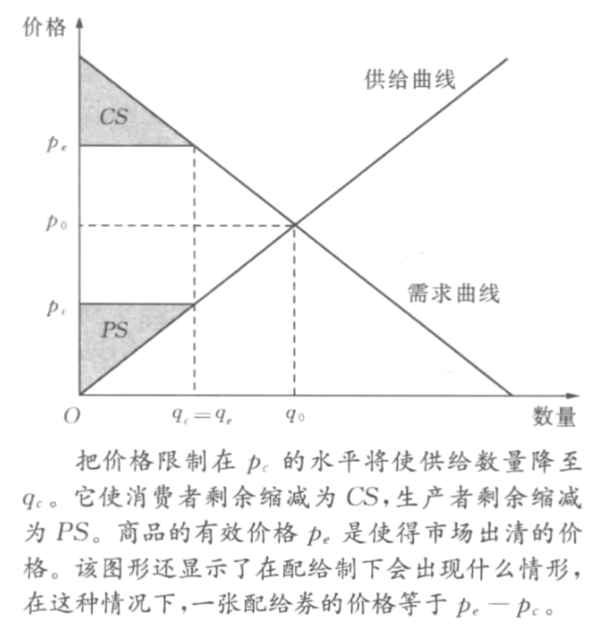
- 需求函数的加总
- 代数法
D(P)=D_1(P)+D_2(P) - 图像法

- 代数法
弹性
- 需求价格弹性
E_P^D=\frac{P}{D}\frac{\mathrm d D}{\mathrm d P}=\frac{\mathrm d \ln D}{\mathrm d \ln P}- 价格变动1\%,需求变动E_P^D\%
- 线性需求函数的弹性
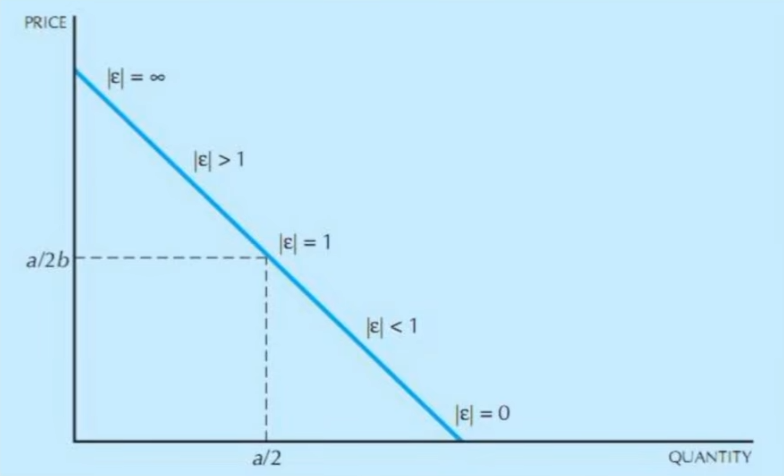
- 商品的需求弹性
|E_P^D|\gt 1称商品是有弹性的需求,降价能增加收入
|E_P^D|= 1称商品是单位弹性的需求
|E_P^D|\lt 1称商品是缺乏的需求 - 不变需求价格弹性
Q=kP^{\varepsilon}\quad\Rightarrow\quad E_P^D=\varepsilon
- 销售收入弹性
E_P^R=\frac{P}{R}\frac{\mathrm d R}{\mathrm d P}=\frac{P}{PD}\frac{\mathrm d PD}{\mathrm d P}=\frac{1}{D}\frac{D\mathrm d P+P\mathrm d D}{\mathrm d P}=1-|E_P^D|- 若|E_R^D|\lt 1: 弹性小说明对价格不敏感,提价消费者照样买
- 若|E_R^D|\gt 1: 弹性大说明消费者对价格非常敏感,稍微提价就都不买了
- 销售产量弹性
E_D^R=\frac{D}{R}\frac{\mathrm d R}{\mathrm d D}=\frac{D}{PD}\frac{\mathrm d PD}{\mathrm d D}=\frac{1}{P}\frac{D\mathrm d P+P\mathrm d D}{\mathrm d D}=1-\frac{1}{|E_P^D|}- 若|E_D^R|\lt 1: 弹性小,提升销量收益减少,说明价格大幅下降
- 若|E_D^R|\gt 1: 弹性大,提升销量收益增大,说明价格基本没变
- 需求收入弹性
E_M^D=\frac{M}{D}\frac{\mathrm d D}{\mathrm d M}=\frac{\mathrm d \ln D}{\mathrm d \ln M}- 若E_M^D\lt 1: 必需品
- 若E_M^D\gt 1: 奢侈品
市场均衡
均衡分析
- 市场供给
- 利润函数\pi=PQ-C(Q)
- 反供给函数\pi^\prime=P-C^\prime(Q)=0\Rightarrow P=C^\prime(Q),图像为市场供给曲线
- 供给函数: P=C^\prime(Q)\Rightarrow S=S(P)
- 市场均衡
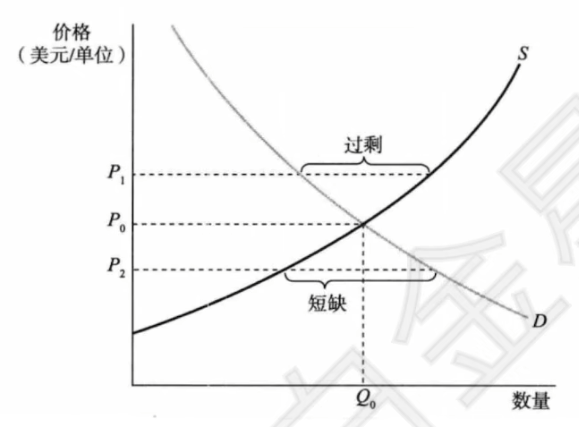
- 比较静态分析
税收
- 税收下的均衡
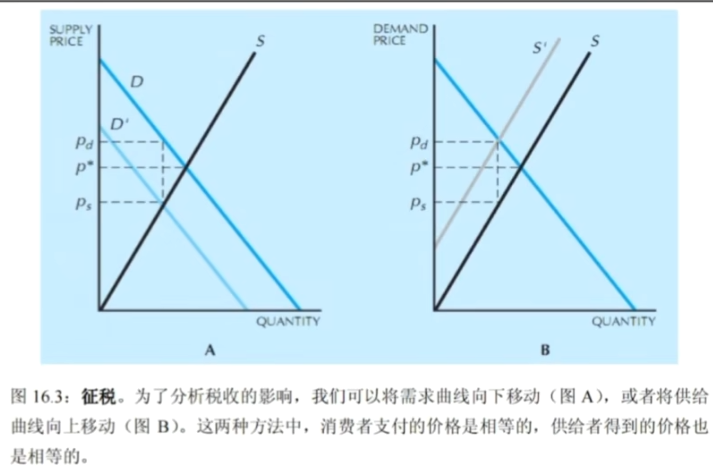
- 图像法
- 代数法
消费者征税: P=P_D(Q)\Rightarrow P=P_D(Q) -t
生产者不变: P=P_S(Q)
新均衡条件: P_D(Q)-P_S(Q)=t
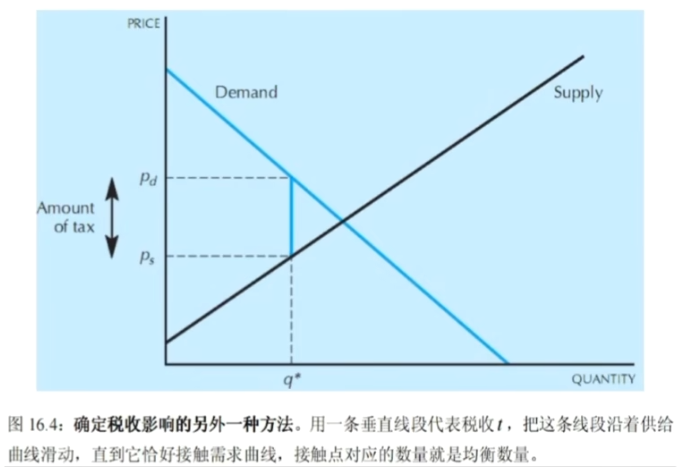
- 图像法
- 税收转嫁
- 消费者承担: P_D-P^\ast,生产者承担: P^\ast-P_S
- 二者承担比率取决于二者曲线斜率之比
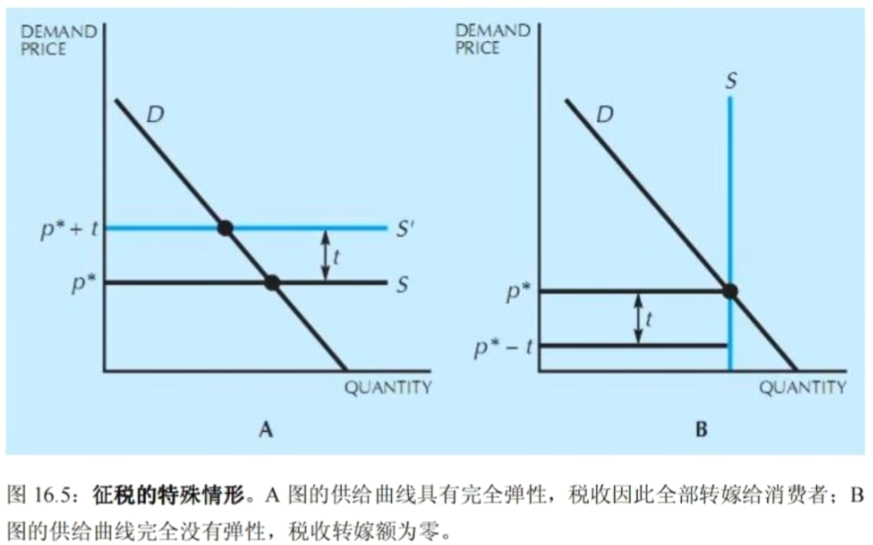
- 税收损失
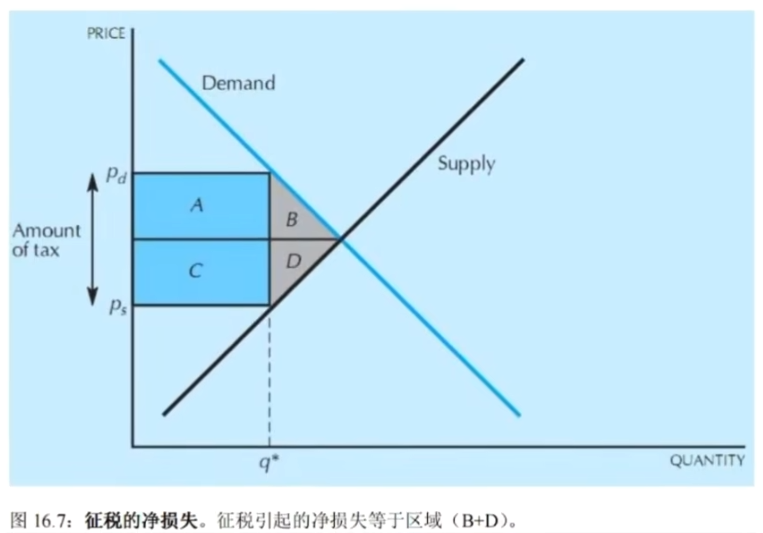
生产者
投入与产出
- 生产函数y(L,K)
- 投入劳动力L和资本K下的产出
- 边际产量
- MP_1=\frac{\partial y}{\partial x_1}=y^\prime_1(x_1,x_2); MP_2=\frac{\partial y}{\partial x_2}=y^\prime_2(x_1,x_2)
- 先增后减,最终增加要素投入带来的边际产出越来越少
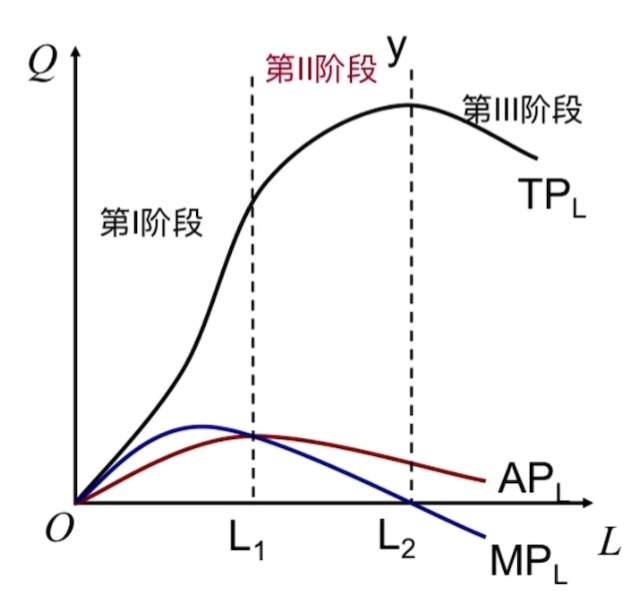
- 边际替代率
- MRTS_{12}=\frac{\mathrm d x_2}{\mathrm d x_1}=-\frac{MP_1}{MP_2}
- 保持产量不变,减少一单位x_1需要增加多少x_2
- 假设等产量线凸向原点,边际替代率递减,增加一种要素需要放弃越少的另一种要素
- 长期与短期
- 短期要素可变,长期要素短期不变长期可变
- 规模报酬
- 规模报酬不变: y(tx_1,tx_2)=ty(x_1,x_2)
- 规模报酬递增: y(tx_1,tx_2)\gt ty(x_1,x_2)\quad t\gt1
- 规模报酬递减: y(tx_1,tx_2)\lt ty(x_1,x_2)\quad t\gt1
成本最小化
- 成本最小化问题
\min_{x_1,x_2} \omega_1x_1+\omega_2x_2\quad\mathrm{s.t.}\quad y(x_1,x_2)=\bar y- MRTS_{12}=-\frac{MP_1}{MP_2}=-\frac{\omega_1}{\omega_2}
- 条件要素需求函数: x_1(\omega_1,\omega_2,\bar y),x_2(\omega_1,\omega_2,\bar y)
- (长期)成本函数: c=\omega_1x_1+\omega_2x_2=c(\omega_1,\omega_2,\bar y)
- (长期)生产扩展线: \frac{MP_1}{MP_2}=\frac{\omega_1}{\omega_2}\Rightarrow f(x_1,x_2)=0
- 生产扩展线f(x_1,x_2)代入生产函数消元得到单个要素的长期投入函数x_1(\bar y),x_2(\bar y),进而求出长期成本函数c(\omega_1,\omega_2,\bar y)=\omega_1x_1(\bar y)+\omega_2x_2(\bar y)
- 显示成本最小化
- \frac{\partial x_1}{\partial \omega_1}总是小于0
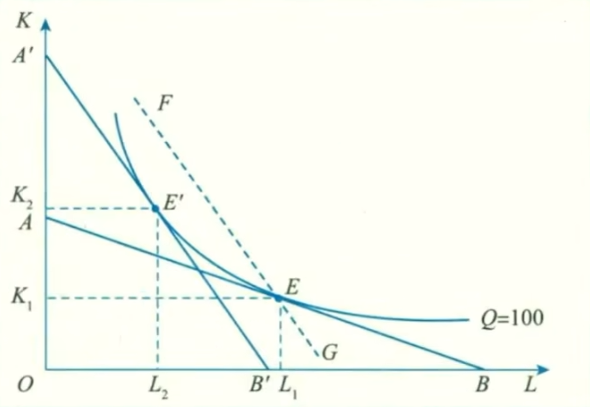
- \frac{\partial x_1}{\partial \omega_1}总是小于0
- 规模报酬
- 平均成本: AC(y)=\frac{c(y)}{y}
规模报酬不变\Rightarrow平均成本不变
规模报酬递增\Rightarrow平均成本递减
规模报酬递减\Rightarrow平均成本递增 - 边际成本: MC(y)=\frac{\mathrm d c(y)}{\mathrm d y}
平均成本递减\Leftrightarrow MC(y)\lt AC(y)
平均成本递增\Leftrightarrow MC(y)\gt AC(y)
- 平均成本: AC(y)=\frac{c(y)}{y}
- 长期成本与短期成本
- 当所有要素都能调整时,生产既定产量的最小成本称为长期成本函数;当部分要素能够调整时,生产既定产量的最小成本称为短期成本函数
x_2=\bar x_2\quad\Rightarrow\quad c_s(\bar x_2,\bar y)=\omega_1 x_1^s(\bar x_2,\bar y)+\omega_2\bar x_2 - 令短期成本函数偏导为0,也可以得到长期成本函数
\frac{\partial c_s(\bar x_2,\bar y)}{\partial\bar x_2}=0\quad\Rightarrow \quad {\bar x_2}^\ast=\bar x_2({\bar y})\quad\Rightarrow \quad c({\bar y})=c_s(\bar x_2({\bar y}),{\bar y}) - 长期均衡最优解也可以用同样的方法
x_1^\ast(\omega_1,\omega_2,\bar y)=x_1^s(\bar x_2({\bar y}),\bar y)
- 当所有要素都能调整时,生产既定产量的最小成本称为长期成本函数;当部分要素能够调整时,生产既定产量的最小成本称为短期成本函数
- 固定成本与准固定成本
- 固定成本是指为固定要素支出的成本;准固定成本是指为准固定要素支付的成本
- 准固定要素是指企业决定生产时(y\gt 0)才需要购买的要素
成本曲线
- 成本函数
- 总成本函数: c(y)=c_v(y)+F
- 平均成本函数: AC(y)=\frac{c(y)}{y}
- 平均可变成本函数: AVC(y)=\frac{c_v(y)}{y}
- 平均不变成本函数: AFC(y)=\frac{F}{y}
- 三者关系: AC(y)=AVC(y)+AFC(y)
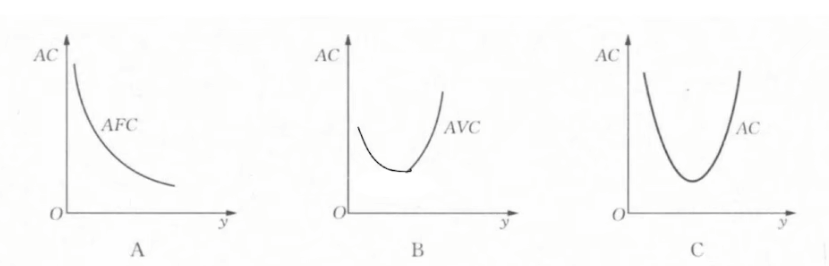
- 长期总成本LTC,长期平均成本LAC,长期边际成本LMC
- 短期总成本STC,短期平均成本SAC,短期边际成本SMC
- 边际成本
- MC(y)=\frac{\mathrm d c(y)}{\mathrm d y}=\frac{\mathrm d c_v(y)}{\mathrm d y}
- AVC(0)=MC(0)
- MC与AC、AVC都交于最低点
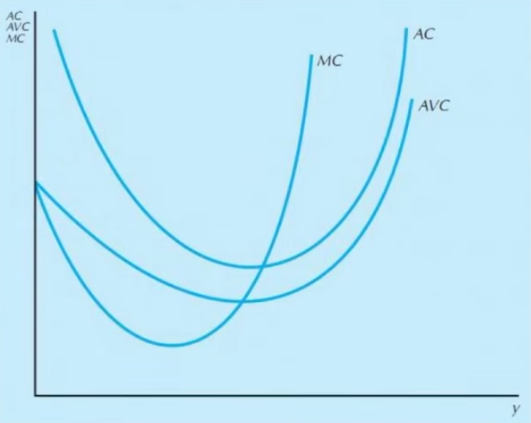
- LAC与SAC的关系
- LAC(y)\le SAC(y),在二次最优化点相切取等
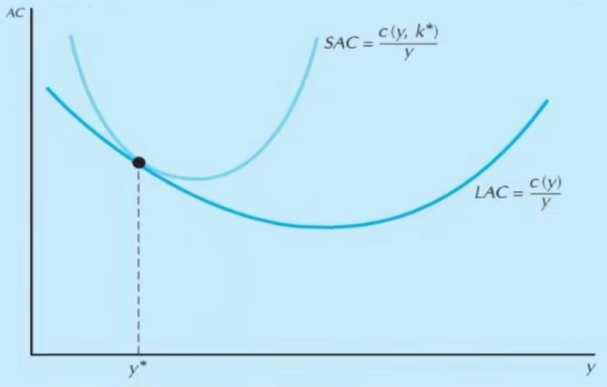
- LAC是SAC的包络线
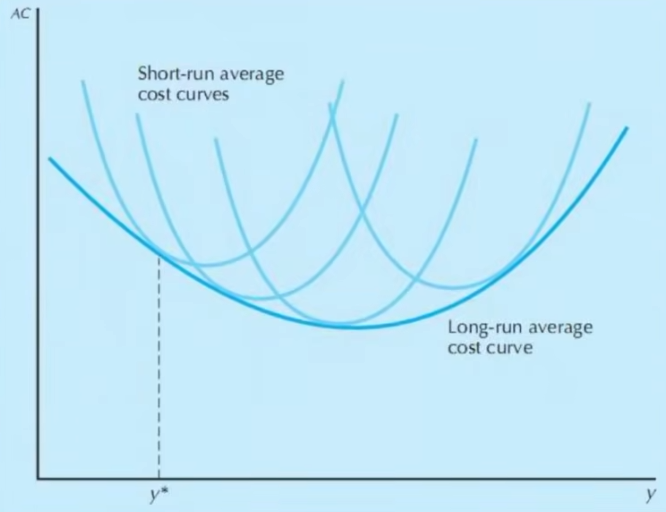
- LAC(y)\le SAC(y),在二次最优化点相切取等
- LMC与SMC的关系
- 两条边际成本经过各自平均成本最低点,且交于y=y^\ast
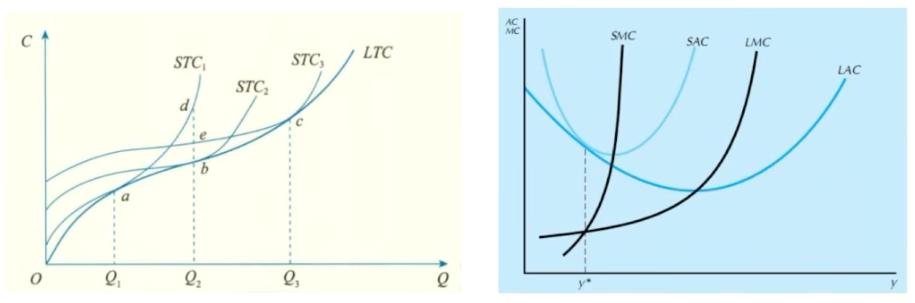
- 两条边际成本经过各自平均成本最低点,且交于y=y^\ast
利润最大化
- 短期利润最大化
\max_{x_1}py(x_1,\bar x_2)-\omega_1x_1-\omega_2 \bar x_2- 一阶条件: MP_1(x_1^\ast,\bar x_2)=\frac{\omega_1}{p}
- 等利润线: \pi=py-\omega_1x_1-\omega_2 \bar x_2\Rightarrow y=y(x_1)
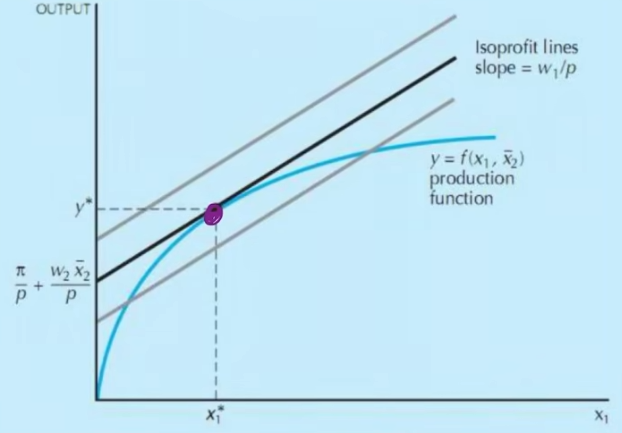
- 比较静态分析
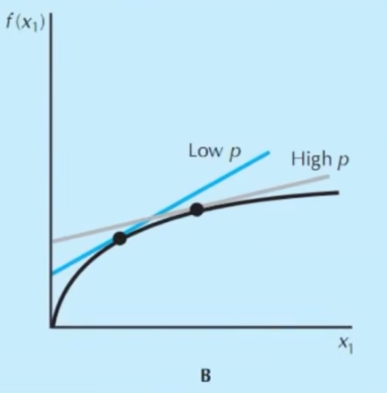
- 提升产品价格
产品价格提升,等利润线变平缓,生产函数图像不变,因此,切点右移,产量上升,纵截距也上升,因此利润上升
- 提升要素价格
要素一的价格提升,等利润线变陡,切点左移,最优要素量下降,产量下降,利润也下降
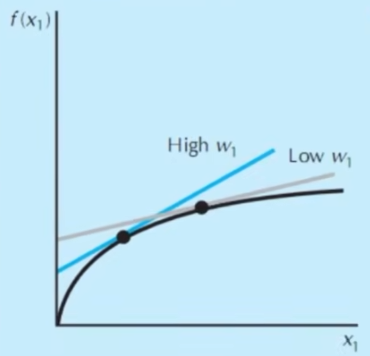
要素二价格提升,不影响等利润线斜率,因此最优投入量不变,产量不变,但利润下降
- 提升产品价格
- 长期利润最大化
\max_{x_1,x_2}py(x_1, x_2)-\omega_1x_1-\omega_2 x_2- 一阶条件: MP_1(x_1^\ast, x_2^\ast)=\frac{\omega_1}{p},MP_2(x_1^\ast, x_2^\ast)=\frac{\omega_2}{p}
- 解得x_1^\ast=x_1(\omega_1,\omega_2,p),x_2^\ast=x_2(\omega_1,\omega_2,p),称为要素需求函数
- 反要素需求曲线
- 根据要素需求函数绘制(x_i,\omega_i)的图像
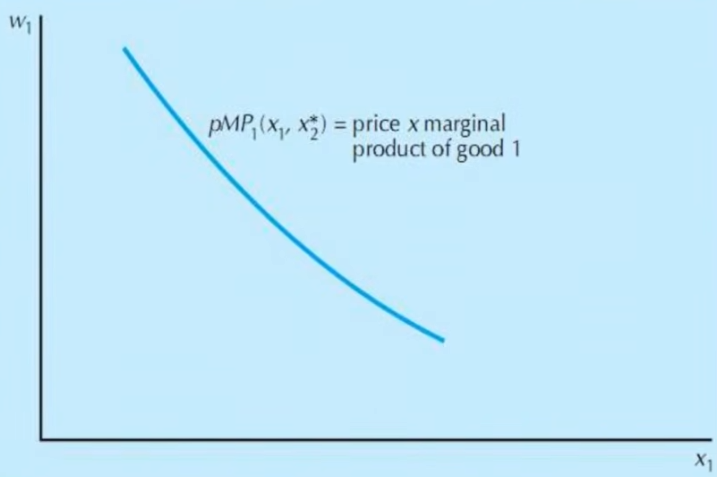
- 根据要素需求函数绘制(x_i,\omega_i)的图像
企业供给
- 竞争性企业的决策供给
\max_Y py-c_v(y)-F- 一阶条件: p=MC(y)
- 根据一阶条件得到供给曲线
- 供给曲线的范围
- MC(y)必须是递增的
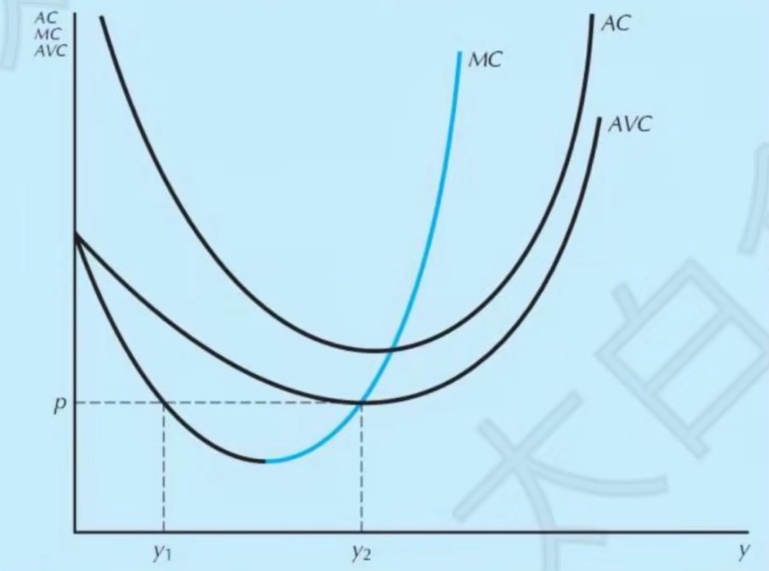
- p\ge AVC(Y)时企业才会选择生产
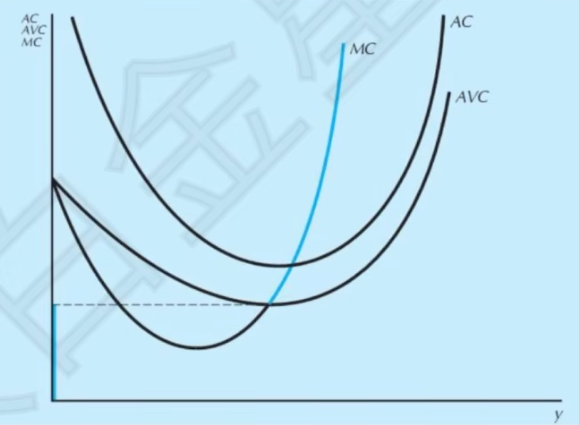
- MC(y)必须是递增的
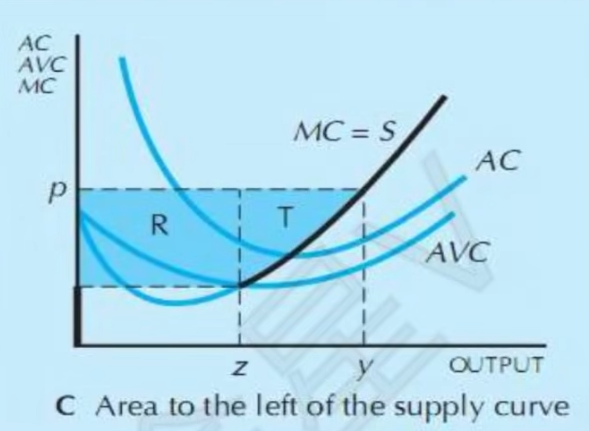
- 利润与生产者剩余
- \pi+F可以用下面两个阴影面积表示
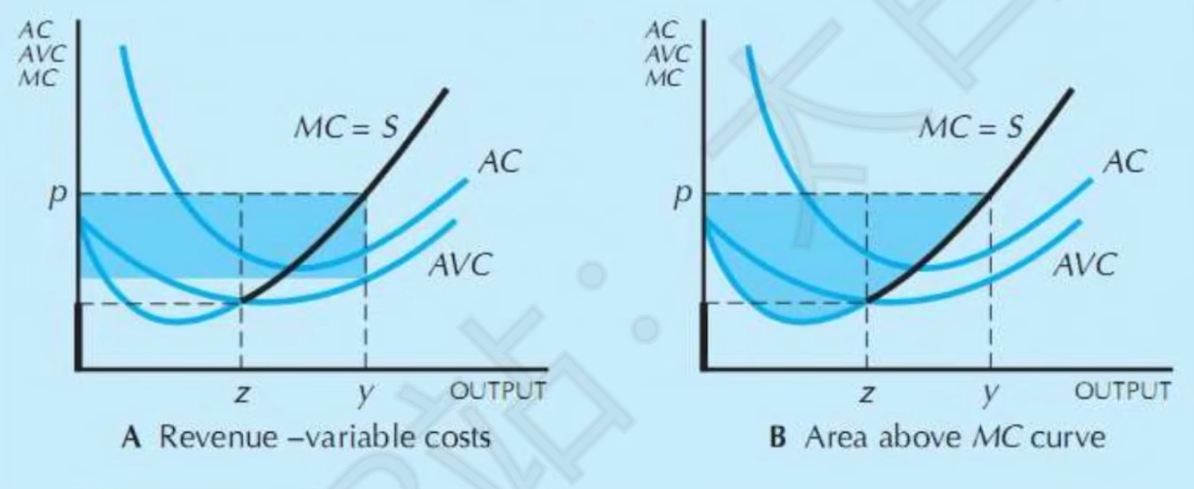
- 生产者剩余,面积也等于\pi+F
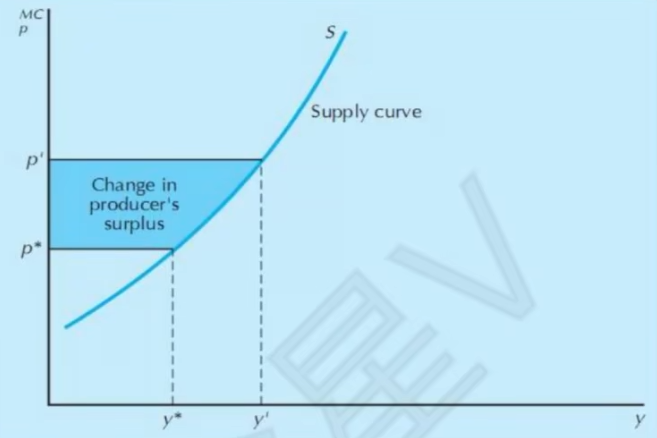
- 生产者剩余的变化
- \pi+F可以用下面两个阴影面积表示
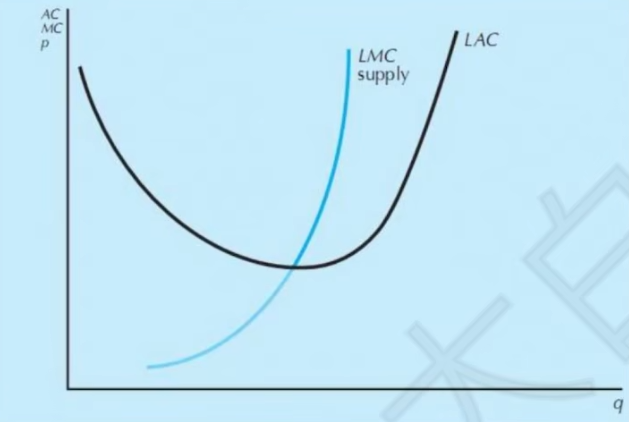
- 长期供给曲线
行业供给
- 短期供给
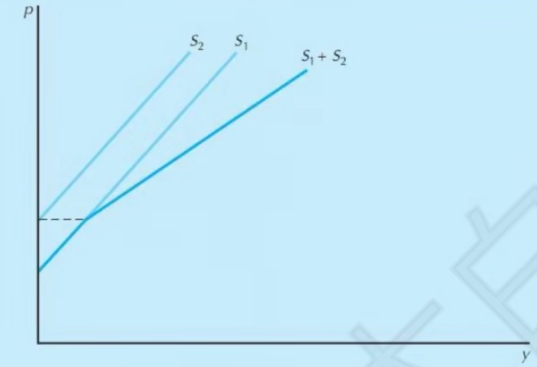
- 供给的加总
- 厂商利润
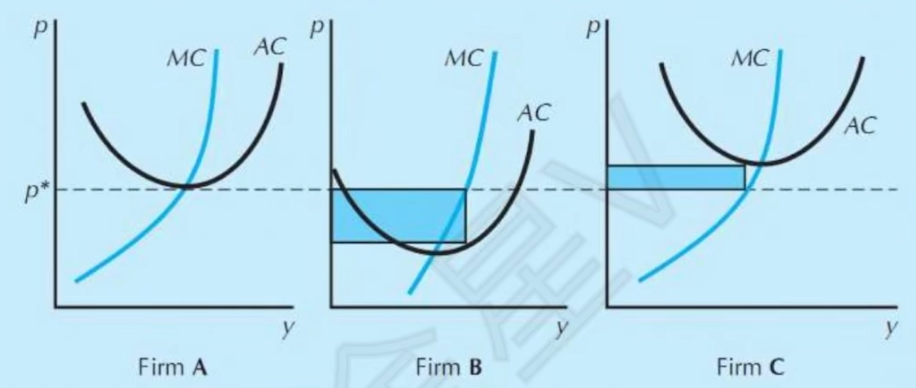
A企业经济利润为零
B企业经济利润为正,数值上为阴影部分面积
C企业亏损。C企业需要判断他的亏损是否超过了固定成本F
- 供给的加总
- 长期供给
- 长期经济利润为0,否则会有新厂商进入,供给增加,价格下降
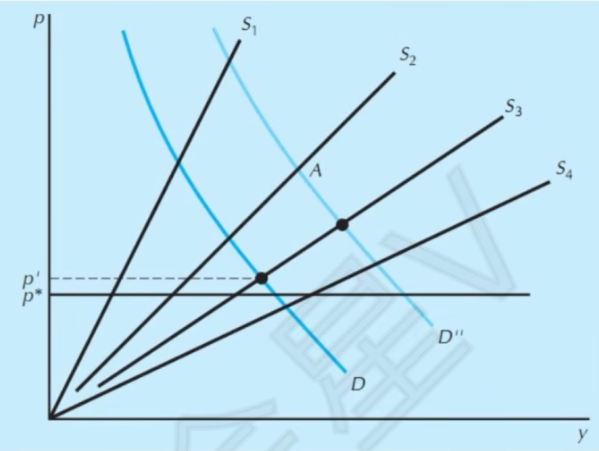
- 考虑厂商出入时的长期供给曲线
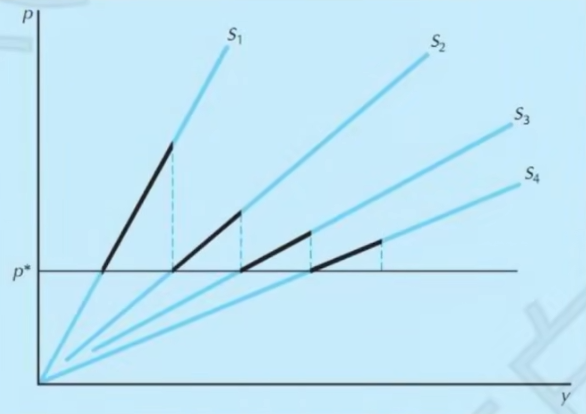
- 假设足够分散,锯齿足够小,长期供给曲线就是水平线,值为最小平均成本
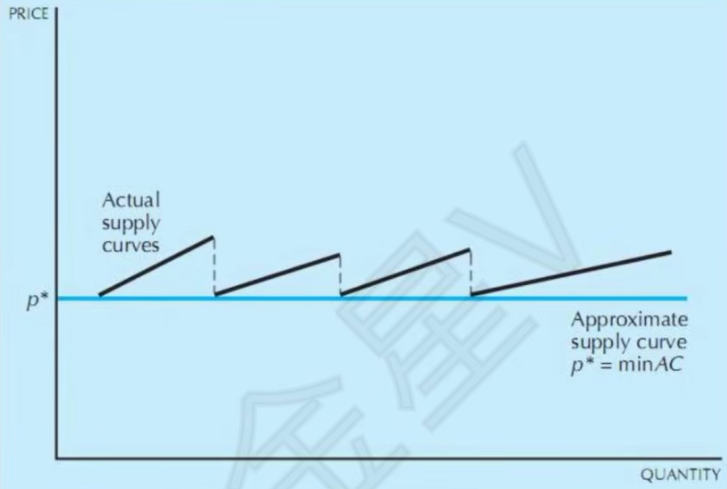
- 长期经济利润为0,否则会有新厂商进入,供给增加,价格下降
- 不变要素
- 不变要素是指供给数量固定不变的要素,可以是长期也可以是短期,可以简单概括为三类:资源类、人才类、许可证类
- 若企业产权允许交易,则长期经济利润依然为0
- 租金
- 经济租金是指企业购买该要素的实际支出金额减去要素供给者能够接受的最低金额
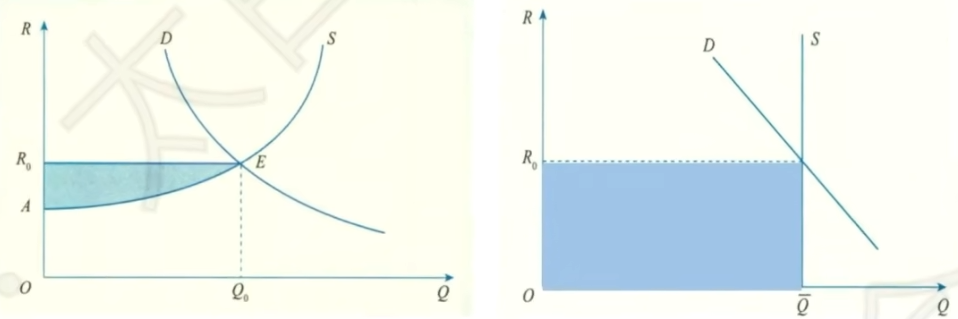
- 存在不变要素时,生产者剩余为\pi+F=0+\omega^\ast Q^\ast=\omega^\ast Q^\ast,等于经济租金
- 经济租金是指企业购买该要素的实际支出金额减去要素供给者能够接受的最低金额
市场结构
垄断
- 利润最大化
\max_y p(y)y-c(y)\quad \Rightarrow \quad p(y)\left(1-\frac{1}{|E_p^y|}\right)=c^\prime(y)- AR(y)=\frac{p(y)}{y}=p(y)
- MR(y)=p(y)\left(1-\frac{1}{|E_p^y|}\right)
- MC(y)=c^\prime(y)
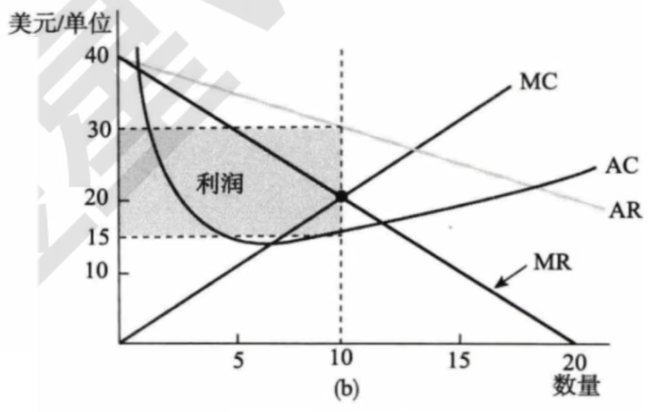
- 勒纳指数
- 垄断厂商如果存在最优产量,必定在富有弹性的产量处生产,即|E_p^y|\gt 1
- 垄断厂商的产品定价总是高于其边际成本,即p^\ast\gt MC(y^\ast)
- 衡量垄断程度: 勒纳指数LI=\frac{p^\ast-MC(y^\ast)}{p^\ast}=\frac{1}{|E_P^D(y^\ast)|}
- 税收
- 数量税
\max_y p(y)y-c(y)-ty\quad \Rightarrow MR=MC^\prime=MC+t
使得MC向上平移t单位
垄断厂商的条件下,税收承担比例不一定
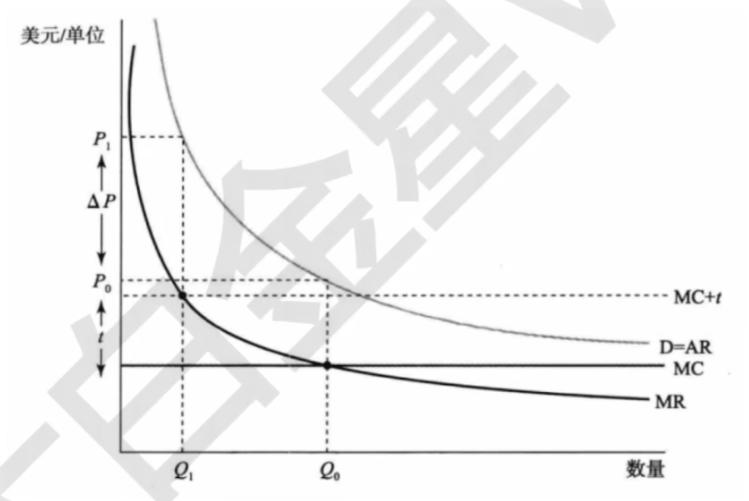
- 价格税
\max_y (1-t)p(y)y-c(y)\quad \Rightarrow \quad MR^\prime=(1-t)MR=MC
使得MR等比例缩放为原先的1-t - 利润税
\max_y (1-t)[p(y)y-c(y)]\quad \Rightarrow \quad MR^\prime=(1-t)MR=MC^\prime=(1-t)MC
不影响均衡条件MR=MC
- 数量税
- 低效率与净损失
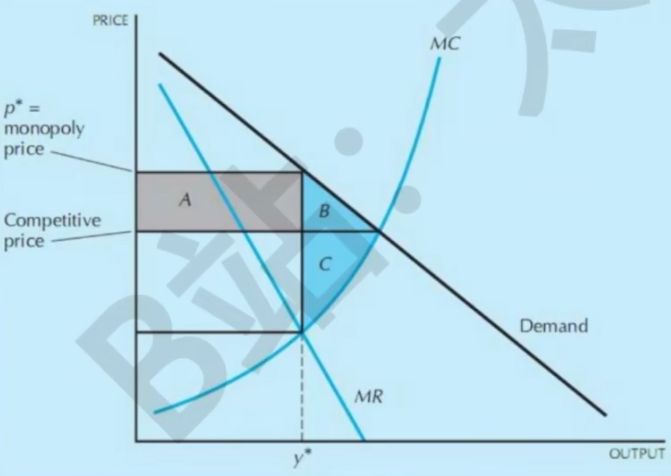
- 垄断损失剩余B+C,消费者剩余损失A+B,生产者获得剩余A-C
- 自然垄断
- 高固定成本: 进入门槛很高导致只有一家企业参与
- 低边际成本: 投产后经营成本低
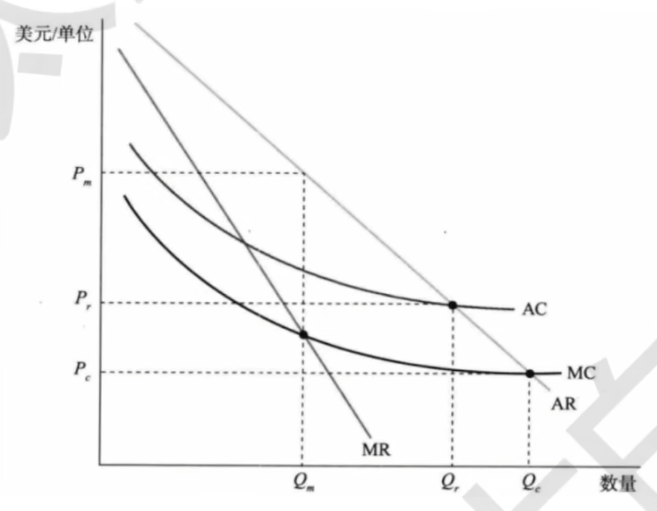
价格歧视
- 三级价格歧视
- 垄断厂商对同一种产品在不同市场上或对不同消费者群体索取不同的价格
\max_{y_1,y_2}p_1(y_1)y_1+p_2(y_2)y_2-c(y_1+y_2)\quad\Rightarrow\quad\frac{p_1}{p_2}=\frac{1-LI_2}{1-LI_1} - 市场需求弹性越小,定价越高
- 垄断厂商对同一种产品在不同市场上或对不同消费者群体索取不同的价格
- 二级价格歧视
- 假设市场中只有两种类型的消费者,但是厂商却不能确认每个具体消费者属于哪一类

- 当线段M=N 时,厂商利润达到最大化
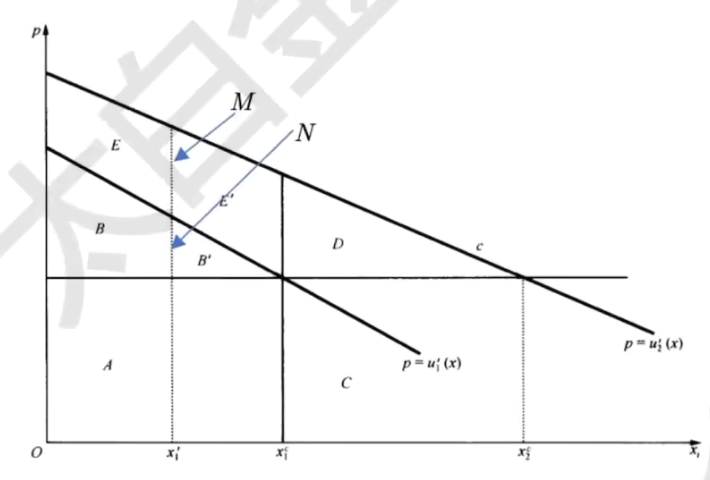
- 假设市场中只有两种类型的消费者,但是厂商却不能确认每个具体消费者属于哪一类
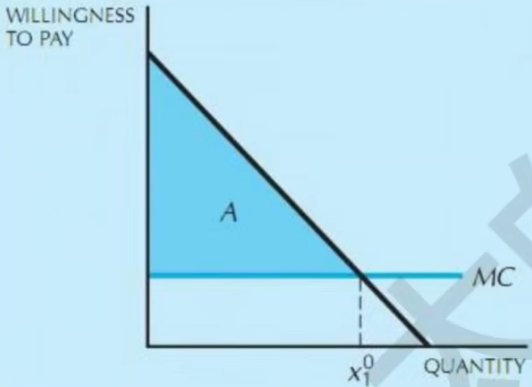
- 一级价格歧视
- 垄断厂商对每个消费者索取他愿意支付的最高价格
- 垄断厂商额外获得消费者总剩余的利润
- 两部收费
- 入门费最多为消费者剩余T,总利润为T+M
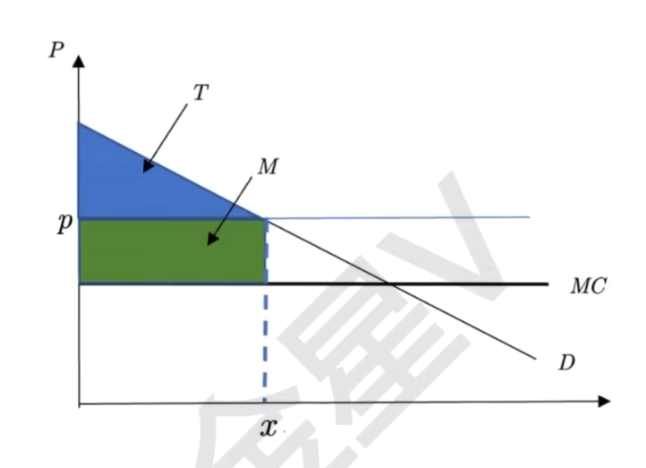
- 两个消费者时,入门费取最小的那个消费者剩余
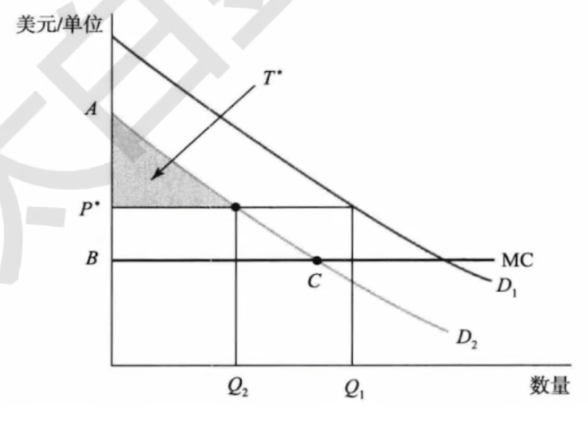 \max_P 2T(P)+(P - C)[Q_1(P)+Q_2(P)]
\max_P 2T(P)+(P - C)[Q_1(P)+Q_2(P)]
- 入门费最多为消费者剩余T,总利润为T+M
寡头
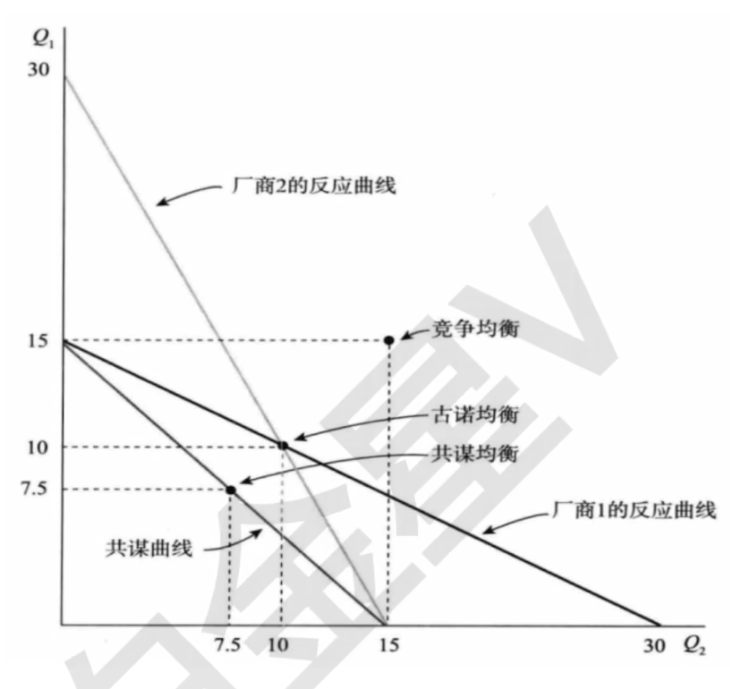
- 古诺模型: 两家厂商对等
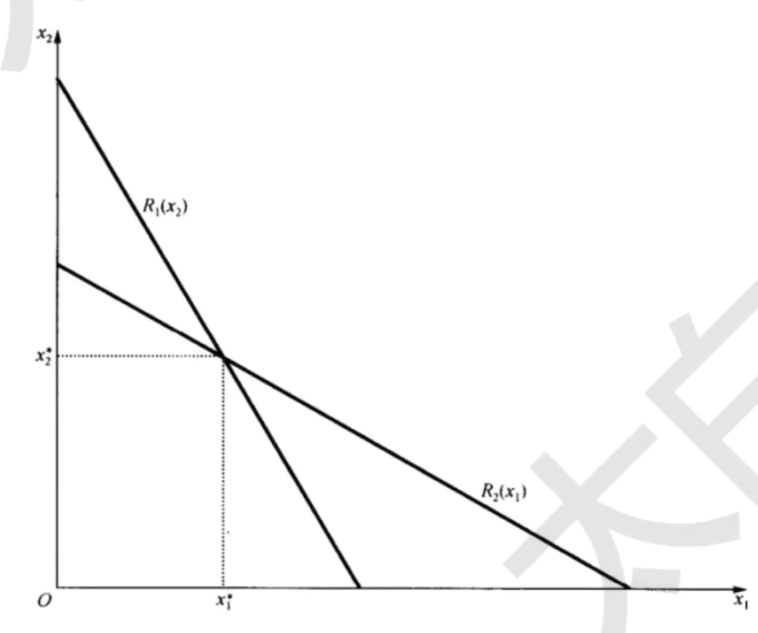
\max_{y_1}p(y_1+y_2^e)y_1-c_1(y_1)- 由一阶条件得到最优反应函数y_1=y_1(y_2^e),y_2=y_2(y_1^e)
- 两个最优反应函数的交点就是古诺均衡
- 斯塔克博格均衡: 厂商一是先行者,先宣布自己的产量,厂商二是追随者
- 等利润线

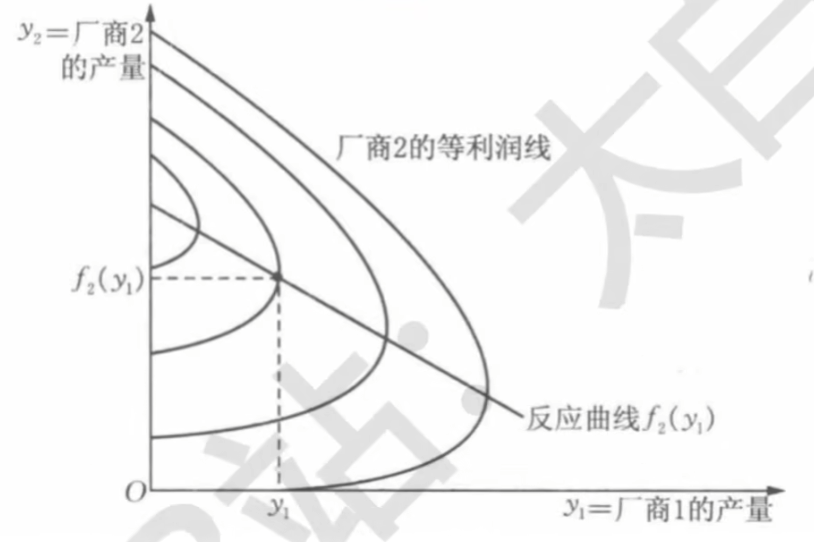
\pi_1=p(y_1+y_2)y_1=[a-b(y_1+y_2)]y_1\quad\Rightarrow \quad y_2=\frac{a}{b}-y_1-\frac{\pi_1}{by_1}
等利润线越靠坐标轴利润越大;反应曲线总是经过等利润线最高点 - 利润最大化
\max_{y_1} p(y_2(y_1)+y_1)y_1-c_1(y_1)
厂商一不仅能控制自己产量y_1,也能使得厂商二产量为y_2(y_1)

- 等利润线
- 共谋
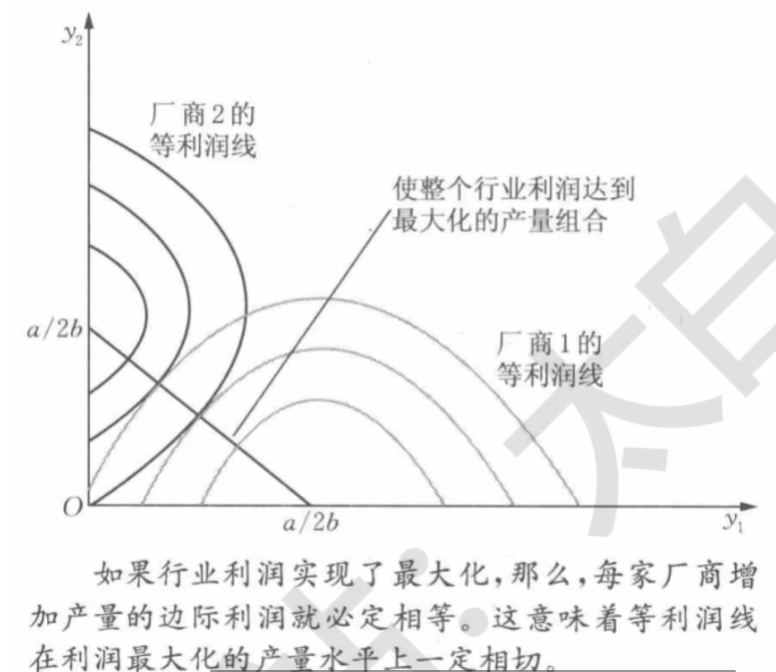 \max_{y_1,y_2}p(y_1,y_2)(y_1+y_2)-c_1(y_1)-c_2(y_2)
\max_{y_1,y_2}p(y_1,y_2)(y_1+y_2)-c_1(y_1)-c_2(y_2)
- 对于厂商一二,增加产出都能获得更多利润
- 波特兰模型
- 两个厂商同时宣布价格,价低者获取全部市场,价格相同则平分市场
- 最终价格都等于边际成本
- 价格领导模型
- 厂商一先宣布价格,厂商二再选择价格
- 此时厂商二将是价格接受者
\max_{x_2} p_1x_2-c_2(x_2)\quad \Rightarrow \quad S(p)=p - 因此厂商一的价格影响厂商二的定价
- 厂商一的剩余需求为D(p)-S_1(p)=a-bp-p=S_1(p)=a-bp_1
\max_{x_1} P(x_1)x_1-cx_1=\max_{x_1}\frac{a-bx_1}{b+1}x_1-cx_1
- 总结
完全竞争
- 从古诺到竞争
\max_{y_i} p(Y)y_i-c_i(y_i)\quad (Y=y_1+\dots+y_n)- 一阶条件为: p(Y)\left(1-\frac{1}{|E_p^Y|}\frac{y_i}{Y}\right)=MC_i(y_i)
- 当厂商足够多,\frac{y_i}{Y}\rightarrow 0,p(Y)=MC_i(y_i)
- 边际收益函数
- 完全竞争: MR=\bar p
- 完全垄断: MR=p(y)\left(1-\frac{1}{|E_p^y|}\right)
- 寡头垄断: MR=p(y)\left(1-\frac{1}{|E_p^Y|}\frac{y_i}{Y}\right)
- 长期的行业供给
- 成本不变的行业供给:具有水平的长期供给曲线
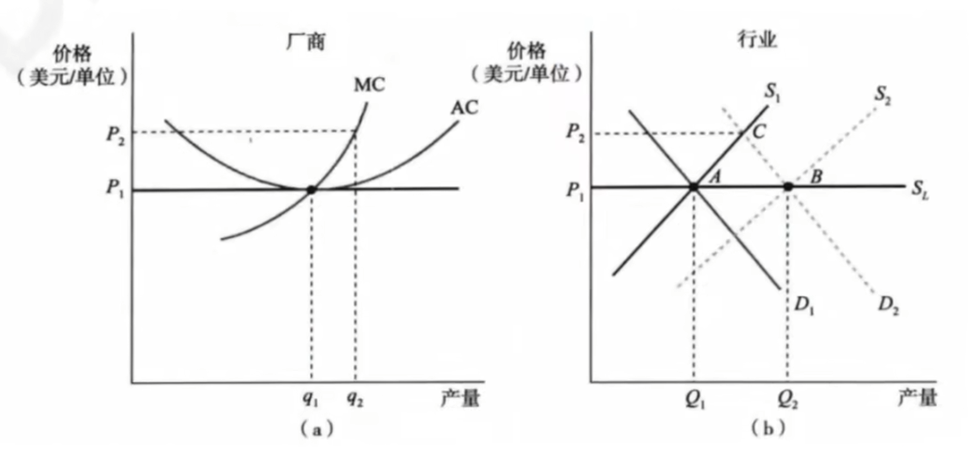
- 成本递增的行业供给:长期供给曲线向右上方倾斜
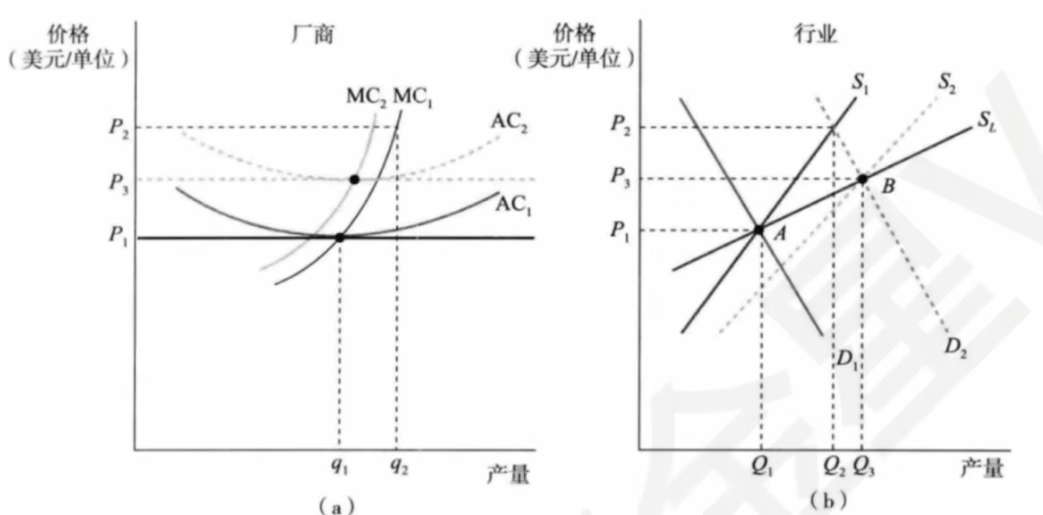
- 成本递减的行业供给:长期供给曲线向右下方倾斜。
- 成本不变的行业供给:具有水平的长期供给曲线
要素市场
- 边际产品收入MRP(x)
- 每增加一单位要素投入给企业带来的收入
MRP(x)=\frac{\mathrm d}{\mathrm d x}R=\frac{\mathrm d }{\mathrm d x}\left[p(y)y\right]=p(y)\left(1-\frac{1}{|E_p^y|}\right)y^\prime=MR(y)MP(x) - 当企业为产品市场竞争性企业,产品价格p(y)为常数
p(y)\equiv \bar p\quad\Rightarrow\quad MRP(x)= \bar p y^\prime=\bar p MP(x)=VMP(x)
VMP(x)又叫边际产品价值 - 对于产品市场垄断性企业总有MRP(x)\lt VMP(x)
在某要素的任何使用水平下,垄断企业的边际产品收入总是小于完全竞争性企业。
给定要素价格,垄断企业的要素使用量也会低于竞争性企业的要素使用量。
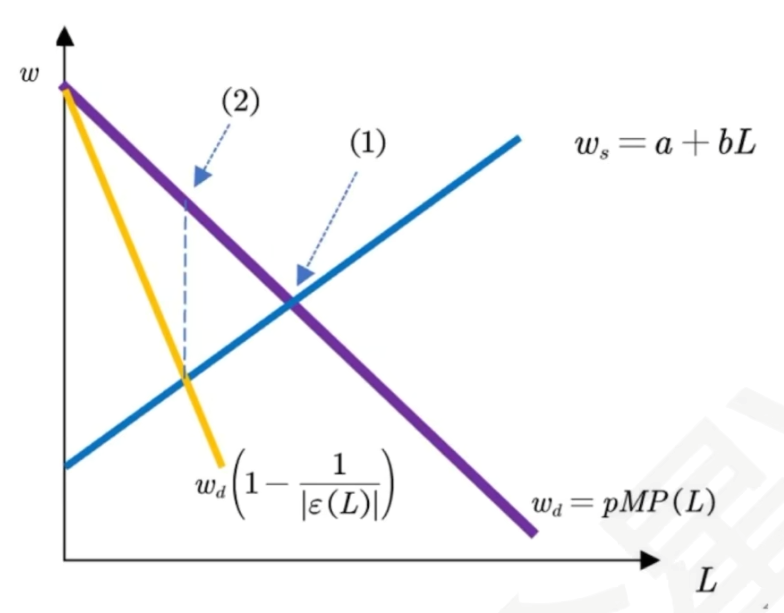
- 每增加一单位要素投入给企业带来的收入
- 边际要素成本MFC(x)
- 每增加一单位要素投入给企业带来的成本
MFC(x)=\frac{\mathrm d}{\mathrm d x}C=\frac{\mathrm d }{\mathrm d x}\left[\omega(x)x\right]=\omega(x)\left(1+\frac{1}{|E_\omega^x|}\right) - 当企业为要素市场价格接受者,要素价格\omega(x)为常数
\omega(x)\equiv \bar\omega\quad\Rightarrow\quad MFC(x)= \bar\omega - 对于要素市场卖方垄断性企业总有MFC(x)\gt \omega(x)
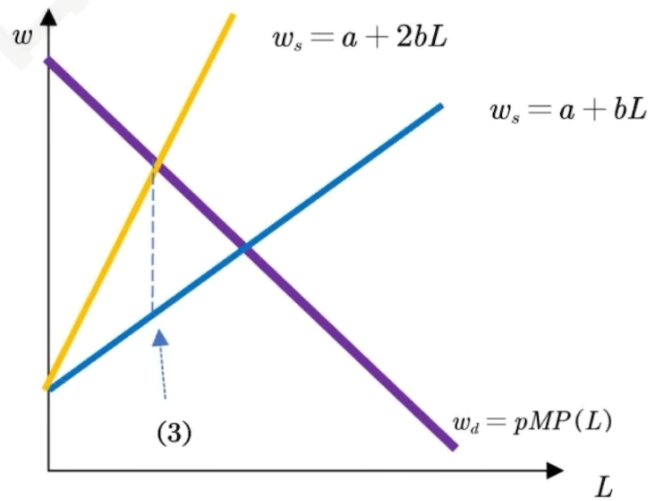
- 每增加一单位要素投入给企业带来的成本
- 均衡条件
MRP(x)=MFC(x)- 交点的横坐标为均衡的要素水平x^\ast,对应的w(x^\ast)为均衡要素价格
- 例如对于产品市场垄断且要素市场卖方垄断的企业
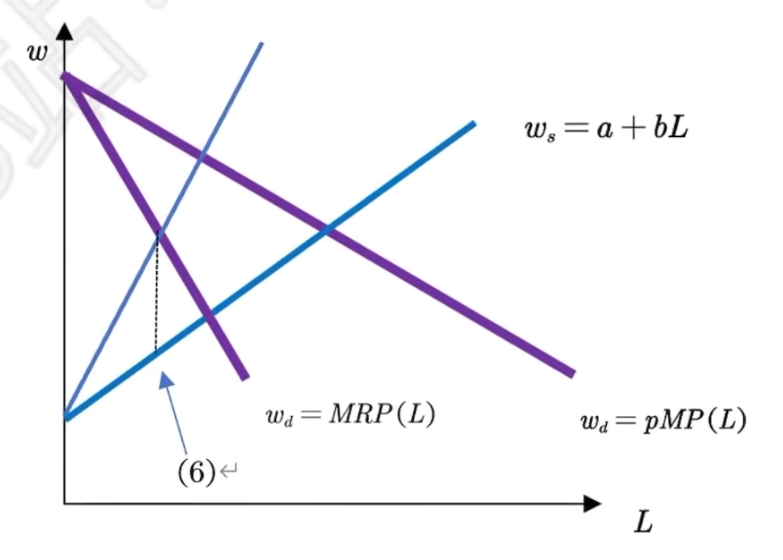
一般均衡
交换
- 埃奇沃斯盒
- 图像
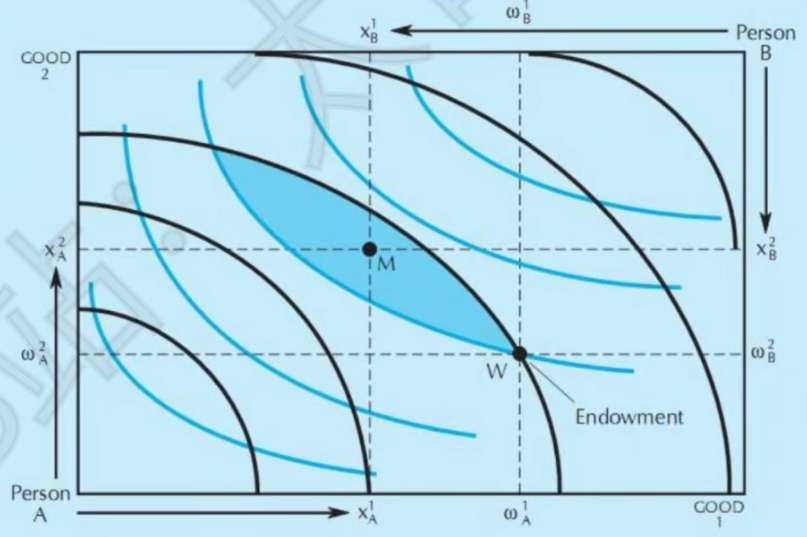
宽度: 商品1的总禀赋\omega^1=\omega^1_A+\omega^1_B
高度: 商品2的总禀赋\omega^2=\omega^2_A+\omega^2_B - 预算约束线
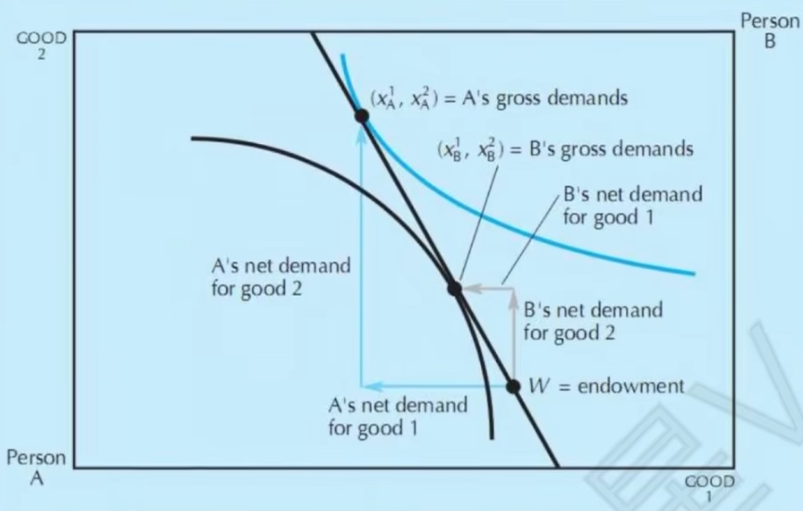
当两个点重合时,市场出清,称为可行配置
- 图像
- 瓦尔拉斯均衡
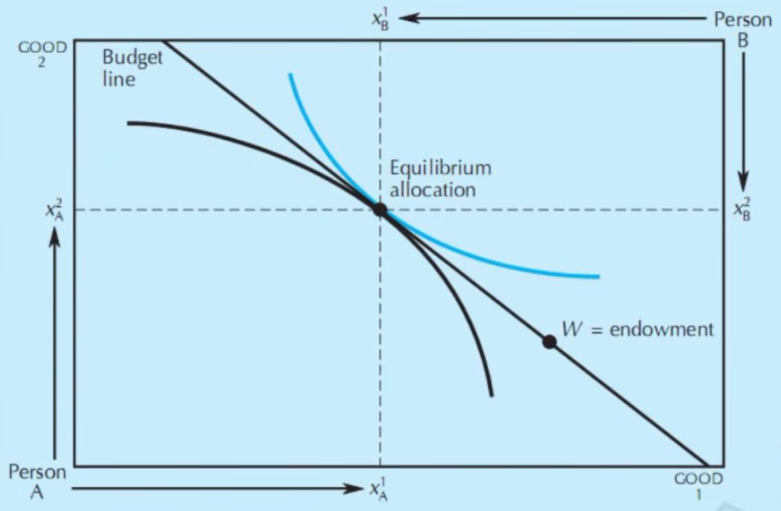
- 无差异曲线在同一点相切
- 瓦尔拉斯均衡存在定理:若消费者的需求函数是连续的,则一定存在瓦尔拉斯均衡
- 瓦尔拉斯法则: 商品1的总超额需求的价值等于商品2总超额供给的价值
- 帕累托有效集
- 两条无差异曲线的切点构成,又叫合同曲线
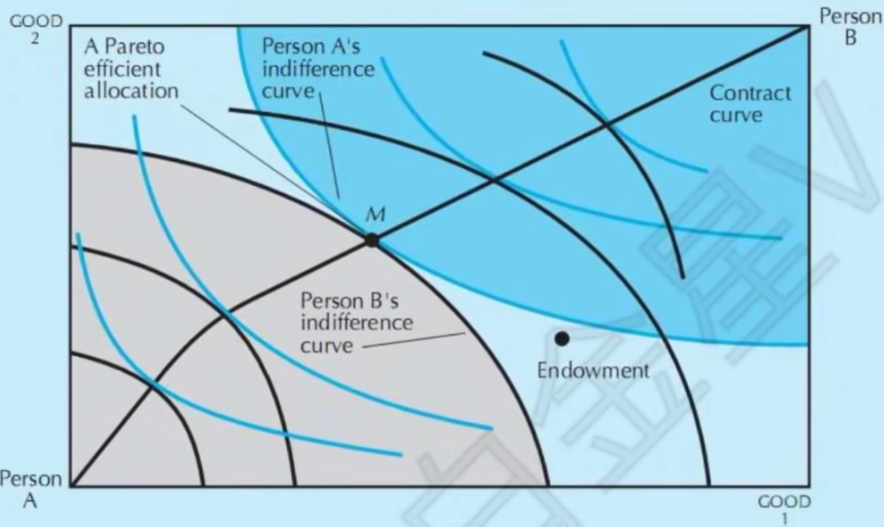
- 不在帕累托有效集的点一定存在帕累托改进
- 瓦尔拉斯均衡要求一定在预算约束线上且分割预算约束线,帕累托有效集不需要
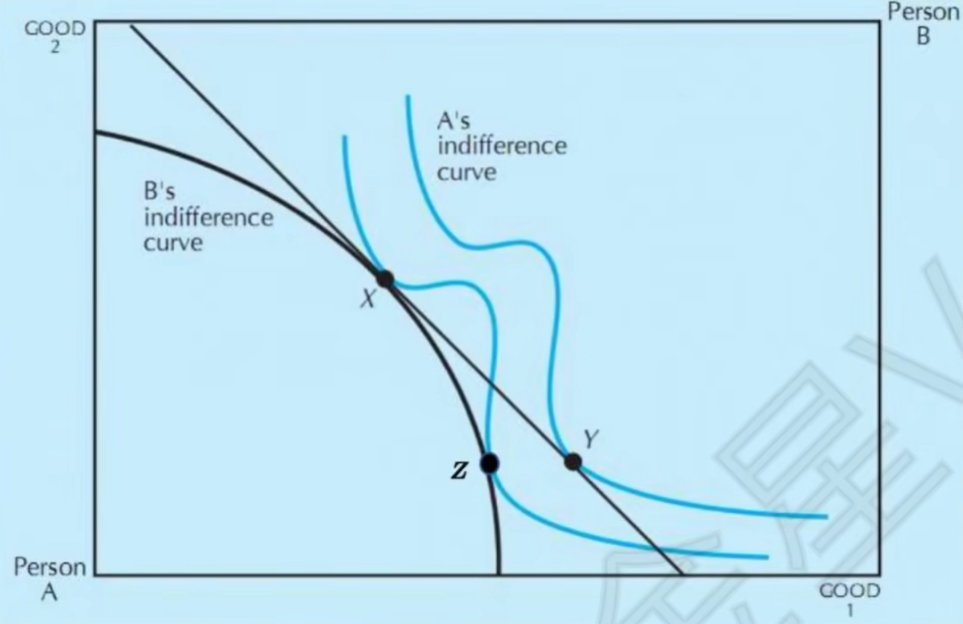
帕累托有效集: X,Z
瓦尔拉斯均衡: 无(A经过X但与预算约束线相交,不满足分割条件)
- 两条无差异曲线的切点构成,又叫合同曲线
- 福利经济学
- 第一定理: 瓦尔拉斯均衡如果存在,必定是帕累托有效的
- 第二定理: 偏好是凸的,则帕累托有效点必是瓦尔拉斯均衡
- 歧视与垄断
- 歧视: 过禀赋点画出被歧视方无差异曲线,歧视方的无差异曲线与其相切
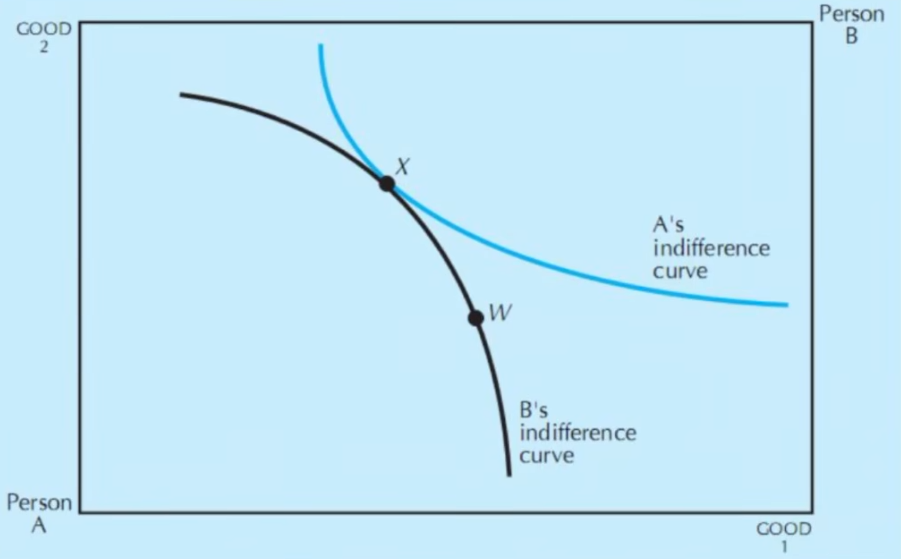
- 垄断: 过禀赋点画出被垄断方需求曲线,垄断方的无差异曲线与其相切
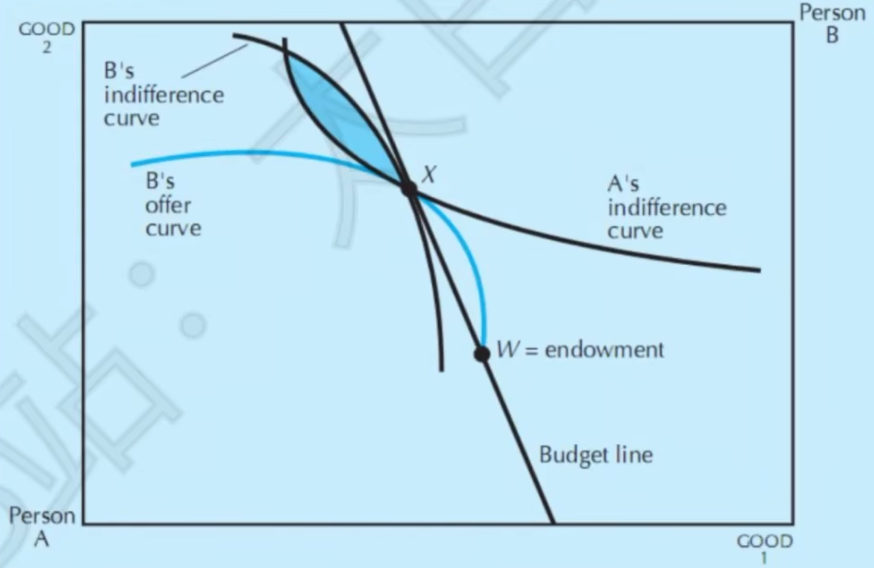
- 歧视: 过禀赋点画出被歧视方无差异曲线,歧视方的无差异曲线与其相切
生产
- 鲁滨逊克鲁索经济
- 既是生产者又是消费者
生产函数C=f(L)
效用函数u=a\ln C+(1-a)\ln(1-L) - 无差异曲线与生产函数相切实现均衡
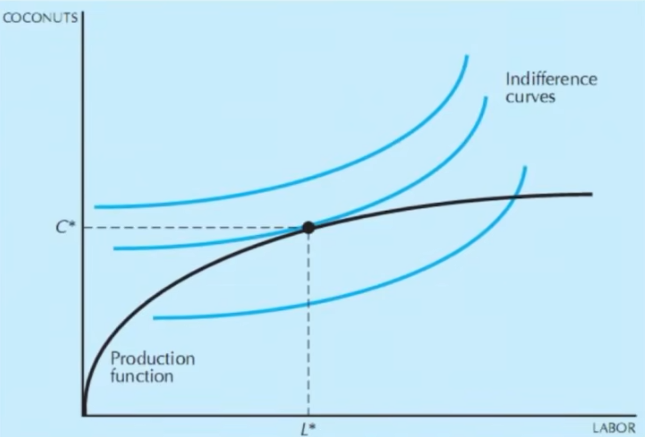
- 利润最大化
\max pf(L)-\omega L\quad\Rightarrow\quad \omega=pMP(L)
- 效用最大化
预算约束线pC=pC^\ast-\omega L^\ast+\omega L\Rightarrow C=\frac{\omega}{p}L+\frac{\pi^\ast}{p}
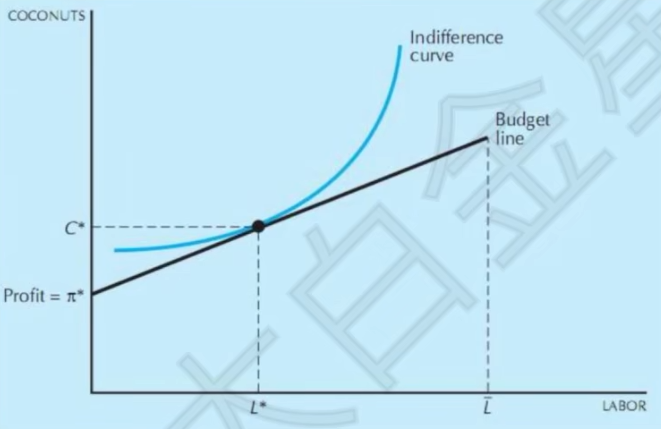
- 总是能找到一条预算约束线分离生产函数和效用函数
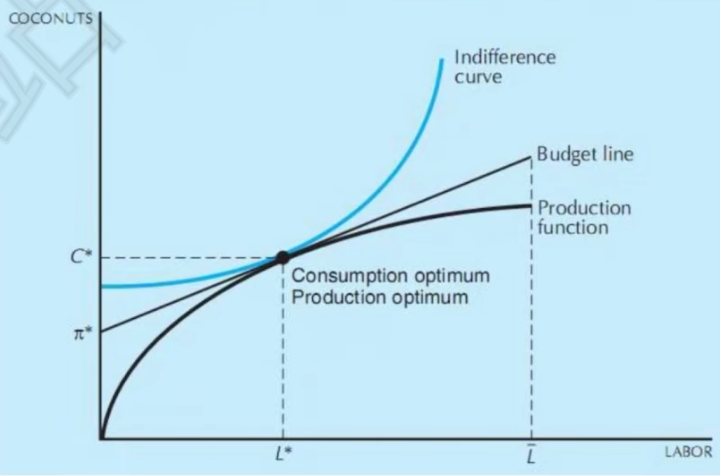
- 既是生产者又是消费者
- 生产可能性
- 存在两个可生产商品,生产函数为C=C(L_C),F=F(L_F),则L=L_C+L_F=C^{-1}(C)+F^{-1}(F),称为生产可能边界
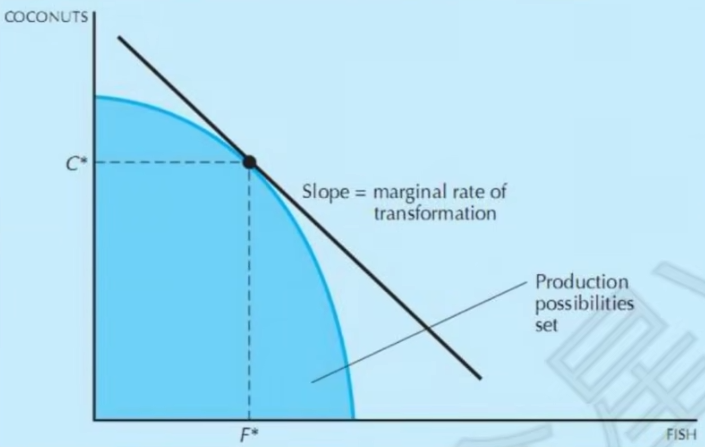
\frac{\mathrm dC}{\mathrm dF}=-\frac{MP_C(L)}{MP_F(L)}
生产契约曲线 - 考虑2个生产者2个生产要素,要素数量给定,使用埃奇沃斯盒分析不同要素分配
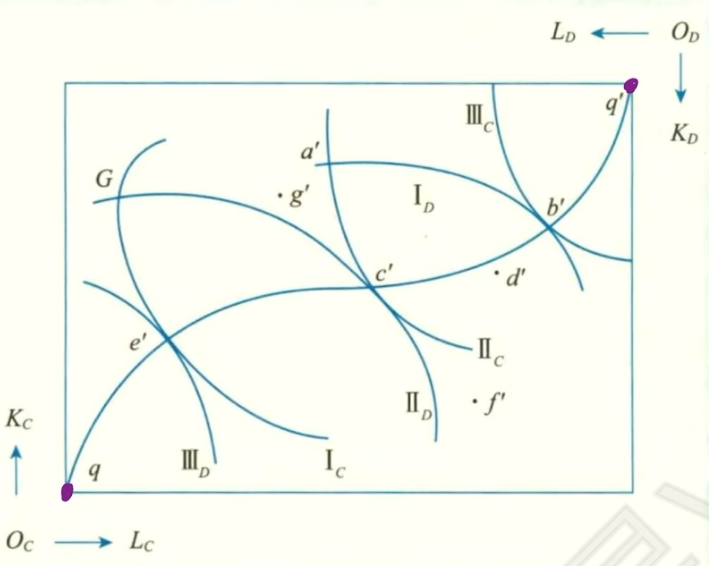
生产可能边界相切时生产最大化,形成的帕累托有效集合称为生产的契约曲线
- 存在两个可生产商品,生产函数为C=C(L_C),F=F(L_F),则L=L_C+L_F=C^{-1}(C)+F^{-1}(F),称为生产可能边界
- 生产-交换均衡(双产品双消费者)
- 生产者
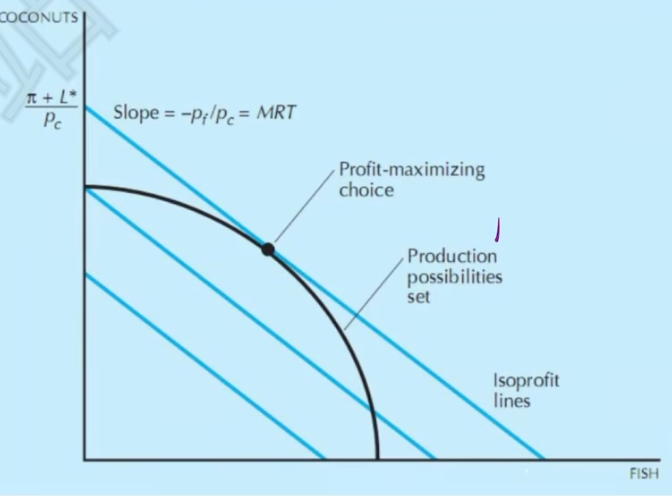
- 消费者
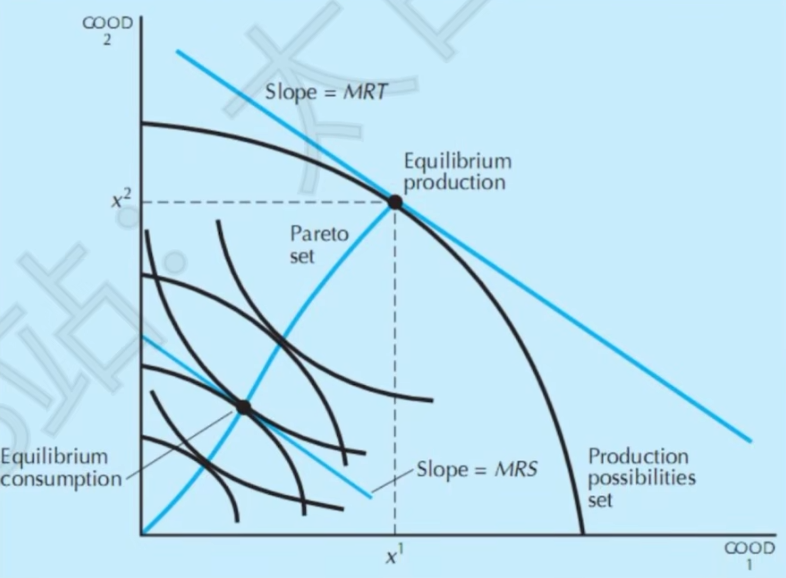
- 生产者