
传统词项逻辑
词项
词项的定义
- 词项是组成命题的基本单位,基本功能是能够充当直言命题中的主项和谓项
- 举例
- 所有的哺乳动物都是脊椎动物
- 有的教师是科学家
词项的内涵和外延
- 内涵:就是词项所反映的对象的本质属性,词项的内涵是词项的质的方面
- 偶数是能够被2整除的数
- 商品是用来交换的劳动产品
- 外延:具有词项所反映的本质属性的对象或对象的总和,词项的外延是词项的量的方面
- 上例中凡是具有“能够被2整除的数”这个本质属性的对象,如4、8、14、26、102、2648等等就是“偶数”这个词项的外延
- 具有“用来交换的劳动产品”这个本质属性的对象,如商场里出售的服装鞋帽、饮品食品、书籍资料、手机电脑等等各种物品就是“商品”这个词项的外延
词项的种类
- 单独词项:指反映某特定对象的词项,或者说外延是一个独无二的对象的词项
- 最高人民法院是中国国家最高审判机关
- 清华大学是一所世界著名的高等学府
- 普遍词项:指称两个或两个以上对象的词项
- 金属是一种具有光泽、富有延展性、容易导电、导热等性质的物质
- 词是最小的能够独立运用的语言单位
- 集合词项:把对象作为集合体反映的整体属性而形成的词项,集合体的个体不一定具有该属性
- 中国人是聪明智慧的
- 犯罪团伙共有13个成员
- 非集合词项:把对象作为类或个体反映而形成的词项,集合体的个体一定具有该属性
- 中国人都应该讲规则。
- 这个犯罪团伙中的犯罪分子会受到处罚。
词项外延之间的关系
- 相容关系:那些两个或两个以上的词项外延至少有一部分重合的关系
- 全同关系/同一关系:所有的S都是P,所有的P都是S,则称S和P之间具有全同关系

几何学里的等边三角形也是等角三角形
- 真包含于关系:所有S都是P,但有些P不是S,称作S真包含于P

育才中学是一所全国重点中学
- 真包含关系:所有P都是S,但有些S不是P,称作S真包含P

司法工作者是包括律师在内的工作群体
- 交叉关系/部分相容关系:有些S是P,但有些S不是P,并且有些P是S,但有些P不是S,则称S和P之间具有交叉关系
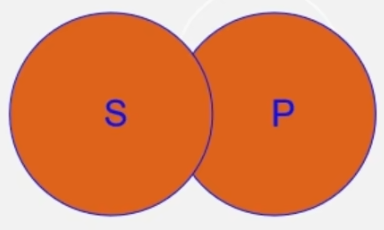
班上同学中有些辩论队队员是体育爱好者
- 全同关系/同一关系:所有的S都是P,所有的P都是S,则称S和P之间具有全同关系
- 不相容关系
- 全异关系/不相容关系:所有S不是P,所有P不是S,则称S和P之间具有不相容关系

学校要求各班级在周六之前必须把教室和寝室的卫生都打扫干净
- 矛盾关系:S、P的外延没有任何部分重合,并且它们的外延之和等于其属词项C的外延,则称S和P之间具有矛盾关系
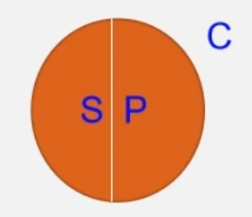
化学元素可以分为金属和非金属
- 反对关系:S、P的外延没有任何部分重合并且它们的外延之和小于其属词项C的外延,则称S和P之间具有反对关系
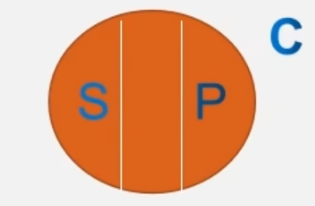
在中国古代文学作品中,唐诗和宋词深受广大群众喜爱
- 全异关系/不相容关系:所有S不是P,所有P不是S,则称S和P之间具有不相容关系
直言命题
- 直言命题是表达一类事物具有或不具有某种性质的命题
- 所有科学家都是知识分孑
- 所有人都是动物。
- 所有金属都是导电的。
- 直言命题的逻辑结构:量项+主项(S)+联项+谓项(P)
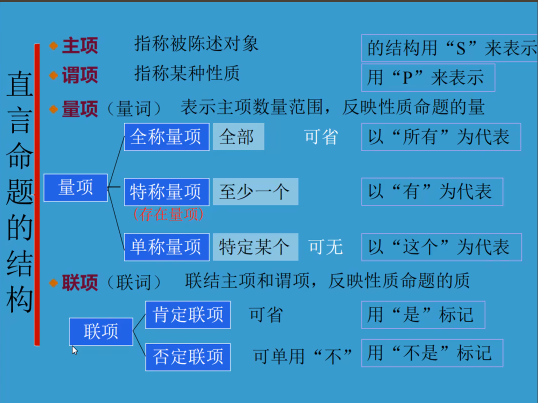
- 量项:规定主项所代表的事物的量的词语
分全称量项(如所有、全部)和特称量项/存在量项(如存在、有的) - 主项:代表被谈论的事物的词项
分单称词项和普遍词项 - 联项:联结主项和谓项的词项
分肯定联项(如是、即)和否定联项(如不是、不会) - 谓项:用于表述主项所代表的事物的性质的词项
- 量项:规定主项所代表的事物的量的词语
- 直言命题的分类:依据不同的分类标准,可将直言命题分为不同的种类。依据联项和量项的不同,可以将直言命题分为以下三大类六种:
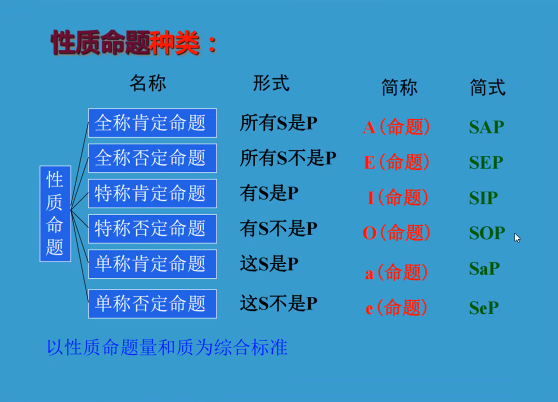
- 全称直言命题
全称肯定直言命题(A命题),其形式为:所有S是P(SAP)
全称否定直言命题(E命题),其形式为:所有S不是P(SEP) - 特称直言命题
持称肯定直言命题(I命题),其形式为:有S是P(SIP)
持称否定直言命题(O命题),其形式为:有S不是P(SOP) - 单称直言命题
单称肯定直言命题(a命题),其形式为:a是P(SaP)
单称否定直言命题(e命题),其形式为:a不是P(SeP)
- 全称直言命题
- 直言命题的周延性
- “周延性”概念用于衡量四种直言命题主项和谓项的外延中的个体是否被全部断定。如果词项外延中的个体在一个直言命题中被全部断定,则称它在该命题中是周延的,否则,它是不周延的
- 判定方法
全称 → 主词周延;特称 → 主词不周延
肯定 → 谓词不周延;否定 → 谓词周延
- 对当方阵
- 对当方阵是传统形式逻辑中对同素材(具有相同主项和谓项)的A、E、I、O四种直言命题在形式上的真假制约关系的刻画。
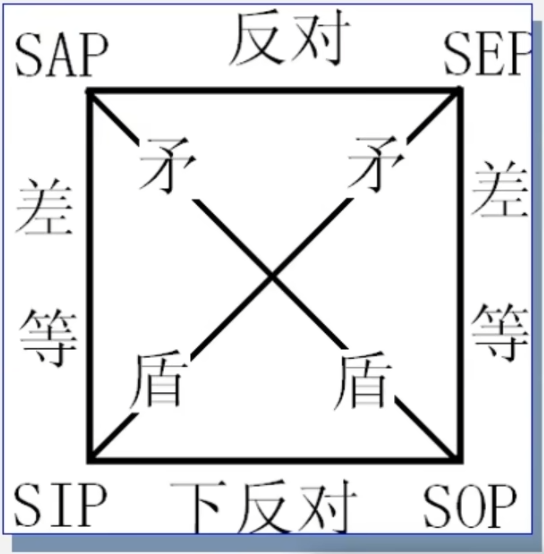
- A命题与O命题矛盾关系:一真一假
- E命题与I命题矛盾关系:一真一假
- A命题与I命题差等关系:A真I真,I假A假
- E命题与O命题差等关系:E真O真,O假E假
- A命题与E命题反对关系:不能同真,可以同假
- I命题与0命题下反对关系:可以同真,不能同假
- 对当方阵是传统形式逻辑中对同素材(具有相同主项和谓项)的A、E、I、O四种直言命题在形式上的真假制约关系的刻画。
直接推理
- 直接推理的定义:以直言命题为前提和结论的推理
- 儿童是未成年人,所以,儿童不是成年人
- 所有猫都是哺乳动物,所以,有的猫是哺乳动物
- 所有人都是要死的,苏格拉底是人,所以,苏格拉底是要死的
- 直接推理的特点
- 只有一个前提。
- 前提和结论的素材相同:具有相同的主项、谓项
- 对当关系推理:根据直言命题之间的对当关系进行的具有必然性的直接推理
- 反对关系:
\begin{align} &SAP\vdash \neg (SEP) \\ &SEP\vdash \neg (SAP) \end{align} - 下反对关系:
\begin{align} &\neg (SIP)\vdash SOP \\ &\neg (SOP)\vdash SIP \end{align} - 矛盾关系:
\begin{align} &SAP\dashv \vdash \neg (SOP) \\ &SOP\dashv \vdash \neg (SAP) \\ &SEP\dashv \vdash \neg (SIP) \\ &SIP\dashv \vdash \neg (SEP) \end{align} - 差等关系:
\begin{align} &SAP\vdash SIP \\ &SEP\vdash SOP \\ &\neg (SIP)\vdash\neg (SAP) \\ &\neg (SOP)\vdash\neg (SEP) \end{align}
- 反对关系:
- 变形推理:通过改变直言命题的质或主谓项位置而进行的直接推理
- 换质推理:换质不换位,谓词负矛盾
\begin{align} &SAP\dashv \vdash SE\bar P \\ &SEP\dashv \vdash SA\bar P \\ &SIP\dashv \vdash SO\bar P \\ &SOP\dashv \vdash SI\bar P \end{align} - 换位推理:换位不换质,变质保周延
\begin{align} &SAP \vdash PIS \\ &SEP\dashv \vdash PES \\ &SIP\dashv \vdash PIS \end{align}
O命题不能换位 - 换质位法
\begin{align} &SAP\dashv \vdash SE\bar P\dashv \vdash \bar PES \\ &SEP\dashv \vdash SA\bar P\vdash \bar PIS \\ &SOP\dashv \vdash SI\bar P\dashv \vdash \bar PIS \end{align}
I命题不能换质位 - 换位质法
\begin{align} &SAP\vdash PIS\dashv \vdash PO\bar S \\ &SEP\dashv \vdash PES\dashv \vdash PA\bar S \\ &SIP\dashv \vdash PIS\dashv \vdash PO\bar S \end{align}
O命题不能换位质
- 换质推理:换质不换位,谓词负矛盾
三段论
- 三段论的定义
- 由两个包含一个共同词项的直言命题作为前提,从而推出一个新的直言命题的推理
- 例如
珍稀动物是应依法加以保护的
大熊猫是珍稀动物
所以,大熊猫是应依法加以保护的
- 三段论的结构
- 两个前提:大前提(包含P)、小前提(包含S)
- 三个项:大项(P)、中项(M)、小项(S)
- 结论为S~P,S在的为小前提,P在的为大前提,M在两个前提均出现
- 三段论规则口诀:中项前提要周延,大项小项莫扩展;一特得特否得否,特否成双结论难
- 中项在前提至少周延一次
中子是基本粒子,有些基本粒子是不带电的;所以,中子是不带电的
基本粒子在小前提大前提都不周延,犯了“中项不周延”错误 - 大项小项在前提中不周延,结论也不能周延;注意:前提中周延了,结论是否周延无所谓
黄马是马,白马不是黄马;所以,白马不是马
马在大前提中不周延,在结论中周延,犯了“大项不当周延”错误 - 前提有特结论特,前提有否结论否
- 两个否定或者两个特称命题都不能使用三段论
- 中项在前提至少周延一次
- 三段论的格和式
- 中项在前提中位置的不同所形成的三段论形式。直言三段论有四个格
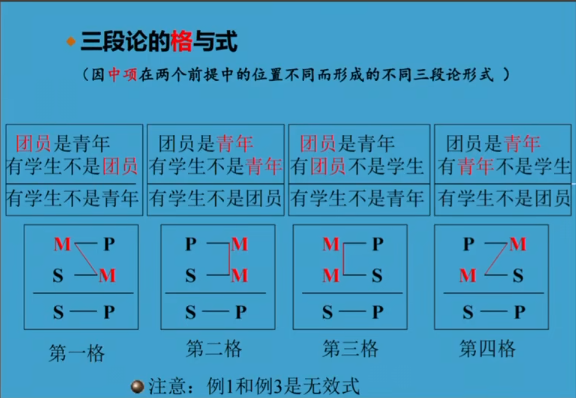
- 直言三段论有64式,有效的只有24式

- 强式口诀:EIOEI AEIOAEIOAEIO IEO
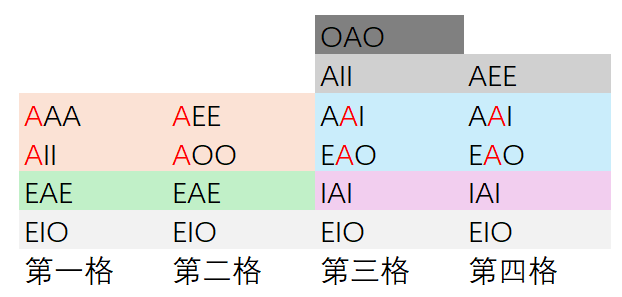
- 中项在前提中位置的不同所形成的三段论形式。直言三段论有四个格
命题逻辑
命题逻辑概述
- 句子与命题
- 有真假的句子所表达的思想是命题
- 一般把“真”和“假”称为命题的真值。
- 在经典逻辑中,只有“真”和“假”,这是逻辑学中的二值原则
- 简单命题与复合命题
- 由词项组成的不包含有其他命题的命题称为简单命题
- 由简单命题通过联结词形成的命题称为复合命题
- 复合命题所包含的命题称为支命题
- 在复合命题中,其联结作用的词称为命题联结词
- 推理
- 推理就是从一些命题推出另一个命题的过程
- 逻辑学重点研究推理形式的有效性
- 一个真实可靠结论有两个条件,一是前提为真,二是推理形式有效
- 命题联结词
- 将支命题联结起来形成复合命题的联结词
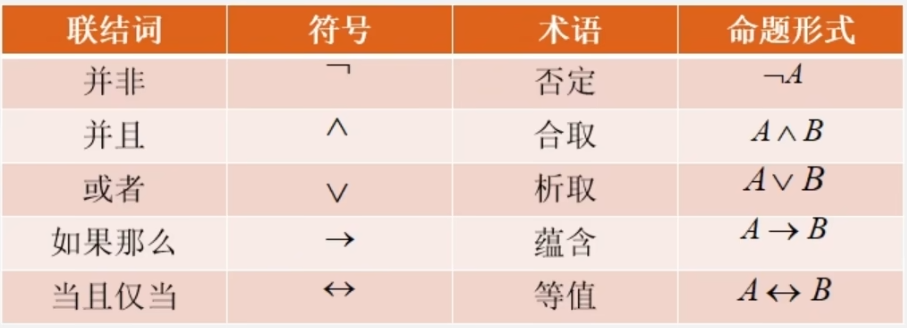
- 根据联结词不同,把复合命题分为:联言命题、选言命题、假言命题、负命题。
- 将支命题联结起来形成复合命题的联结词
- 命题联结词的真值表
- 并非:并非A
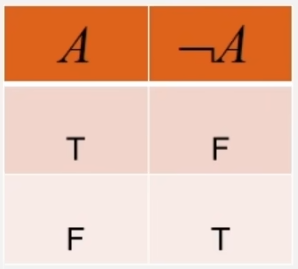
- 合取:A并且B
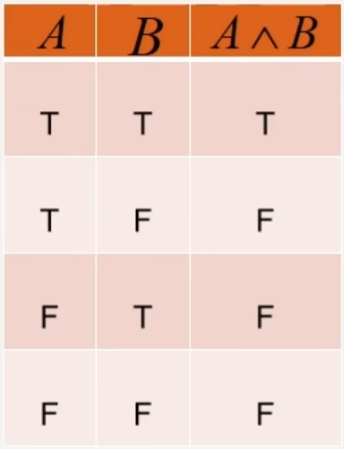
- 析取:A或者B
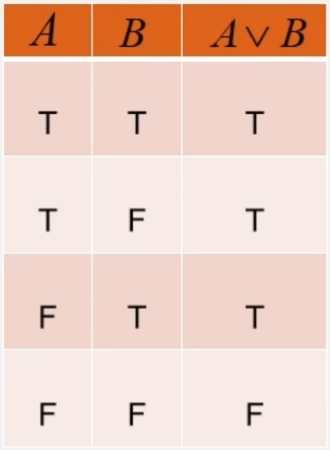
- 蕴涵:如果A那么B
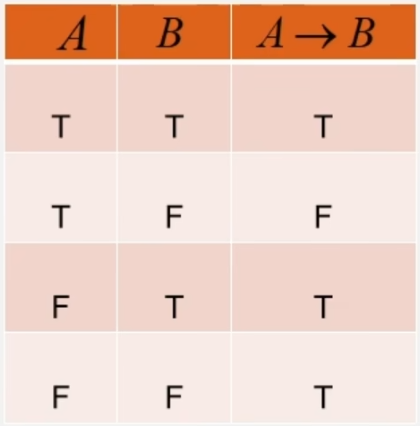
假命题蕴含任何命题
- 等值:A当且仅当B
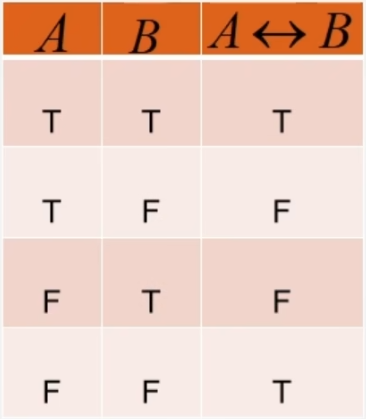
- 并非:并非A
复合命题的推理
- 否定命题
- 否定引入推理:p是真,那么\neg\neg p是真
p\Rightarrow\neg\neg p - 否定消去推理:\neg\neg p是真,那么p是真
\neg\neg p\Rightarrow p
- 否定引入推理:p是真,那么\neg\neg p是真
- 合取命题:“既......又......”"“不仅......而且......”“虽然......但是.....”
- 合取引入推理:p,q是真,那么p\wedge q是真
p,q\Rightarrow p\wedge q - 合取消去推理:p\wedge q是真,那么p,q都是真
\begin{align} &p\wedge q\Rightarrow p \\ &p\wedge q\Rightarrow q \end{align}
- 合取引入推理:p,q是真,那么p\wedge q是真
- 析取命题:"...或...”"可能...可能..."
- 析取引入推理:p或q是真,那么p \vee q是真
\begin{align} &p \Rightarrow p\vee q \\ &q\Rightarrow p\vee q \end{align} - 析取消去推理:p \vee q是真,那么p,q至少一个为真
\begin{align} &p\vee q,\neg p \Rightarrow q \\ &p\vee q,\neg q \Rightarrow p \end{align}
- 析取引入推理:p或q是真,那么p \vee q是真
- 条件命题:“只要...就...”“若...则...”
- 条件引入推理:真命题蕴含任何命题,假命题被任何命题蕴含
\begin{align} &q\Rightarrow p\rightarrow q \\ &\neg p\Rightarrow p\rightarrow q \end{align} - 条件消去推理:肯定前件或否定后件
\begin{align} &p\rightarrow q,p\Rightarrow q \\ &p\rightarrow q,\neg q\Rightarrow \neg p \end{align} - 等价形式:与析取逻辑等值
p\rightarrow q\Leftrightarrow \neg p\vee q
- 条件引入推理:真命题蕴含任何命题,假命题被任何命题蕴含
- 等值命题:“只要/并且/只有...就...”“如果/并且/只有...则...”
- 等值引入推理
\begin{align} p,q\Rightarrow p\leftrightarrow q \\ \neg p,\neg q\Rightarrow p\leftrightarrow q \end{align} - 等值消去推理
\begin{align} p\leftrightarrow q \Rightarrow p\rightarrow q \\ p\leftrightarrow q \Rightarrow q\rightarrow p \end{align} - 等价形式:与条件命题逻辑等值
p\leftrightarrow q \Leftrightarrow (p\rightarrow q)\wedge(q\rightarrow p)
- 等值引入推理
- 负命题
- 连言判断
\neg (p\wedge q)\Leftrightarrow (\neg p\vee\neg q) - 选言判断
\neg (p\vee q)\Leftrightarrow (\neg p\wedge\neg q) - 充分条件假言判断
\neg (p\rightarrow q)\Leftrightarrow (p\wedge \neg q) - 充分必要条件假言判断
\neg (p\leftrightarrow q)\Leftrightarrow (\neg p\wedge q)\vee (p\wedge \neg q)
- 连言判断
- 逻辑等值:p\Rightarrow q,q\Rightarrow p,那么p,q逻辑等值,记为p\Leftrightarrow q或p\dashv \vdash q
真值表方法
- 构造真值表
- 根据n个简单命题确定初始的2^n种真值情况
- 根据简单命题的真值情况从内到外依次确定各个支命题的真值情况,最终确定复合命题的真值情况
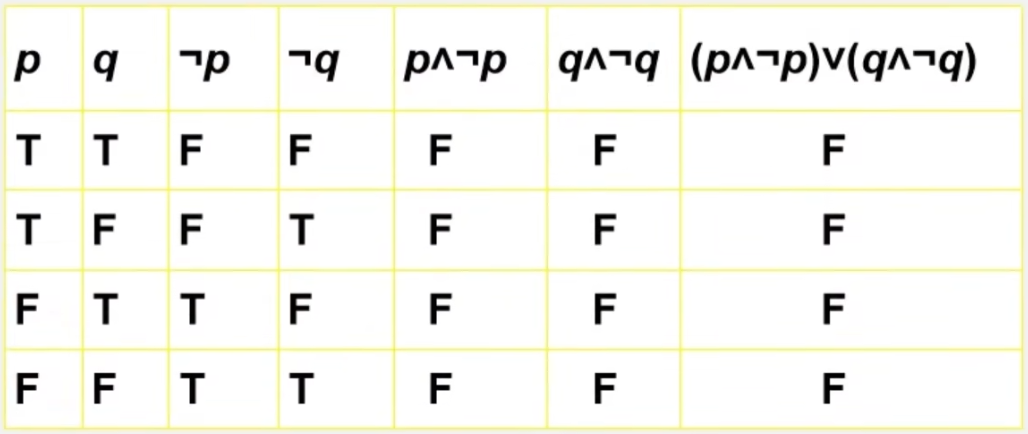
- 真值表的结果
- 重言式:复合命题总为T
- 假言式:符合命题总为F
- 或言式:符合命题既可能是T也可能是F
- 比较2个命题
- p_1,p_2\cdots,p_n\Rightarrow q是有效推理当且仅当p_1\wedge\cdots\wedge p_n\rightarrow q是重言式
- p,q是逻辑等值当且仅当p,q真值表结果相同
其他逻辑
谓词逻辑
- 个体词、谓词和量词
- 个体词:代表个体的词
论域:谈论个体的范围
个体常元:a,b,c,\cdots
个体变元:x_1,x_2,x_3,\cdots
函数符号:f_n(x_1,\cdots,x_n) - 谓词:表达个体的性质或者个体之间的关系
一元谓词:只带有一个项的谓词
二元谓词:表示两个项所代表的个体之间的二元关系
谓词符号:P_n(x_1,\cdots,x_n) - 量词
\forall :论域中所有个体
\exists :论域中存在一个个体
- 个体词:代表个体的词
- 谓词逻辑的形式语言
- 直言命题
单称肯定命题:“a是P”符号化的结果是 “P(a)”
单称否定命题:“a不是P”符号化的结果是“\neg P(a)”
全称肯定命题:“所有S都是P”符号化的结果是“\forall x(S(x)\rightarrow P(x))”
全称否定命题:“所有S都不是P”符号化的结果是“\forall x(S(x)\rightarrow \neg P(x))”
特称肯定命题:“有的S是P”符号化的结果是“\exists x(S(x)\wedge P(x))”
特称否定命题:“有的S不是P”符号化的结果是“\exists x(S(x)\wedge \neg P(x))” - 嵌套量词
每个人都爱某些人:\forall x(P(x)\rightarrow \exists y(P(y)\wedge L(x,y)))
有些人爱所有人:\exists x(P(x)\wedge \forall y(P(y)\rightarrow L(x,y)))
有些人不爱任何人:\exists x(P(x)\wedge \forall y(P(y)\rightarrow \neg L(x,y))) - 数量命题
至少有1个个体:\exists x(\cdots)
至少有2个个体:\exists x\exists y(x\not\equiv y\wedge\cdots)
至少有3个个体:\exists x\exists y\exists z(x\not\equiv y\wedge x\not\equiv z\wedge y\not\equiv z\wedge\cdots)
至多有1个个体:\forall x\forall y(\cdots\rightarrow x\equiv y)
至多有2个个体:\forall x\forall y\forall z(\cdots\rightarrow x\equiv y\vee y\equiv z\vee x\equiv z )
至少有2个S是P:\exists x\exists y(x\not\equiv y\wedge S(x)\wedge P(x)\wedge S(y)\wedge P(y))
至多有1个S是P:\forall x\forall y(S(x)\wedge P(x)\wedge S(y)\wedge P(y)\rightarrow x\equiv y)
- 直言命题
传统归纳逻辑
- 归纳推理的定义
- 以个别或特殊性知识为前提,推出一般性知识的推理。它反映了人们对客观事物的认识是从个别事物开始,进而认识事物的普遍规律的思维过程
- 归纳推理的作用
- 归纳推理是发现真理和获取新知的手段
- 归纳推理是说明和论证问题的方法
- 枚举归纳推理
- 从若干个别性前提得出全称性结论的推理
A地的原始文化与非洲原始文化相同;B地的原始文化与非洲原始文化相同;C地的原始文化与非洲原始文化相同;... → 人类的祖先产生于非洲 - 枚举归纳推理不具有完全的可靠性,为提高枚举归纳推理结论的可靠性,我们应注意以下两点:
被考察对象的数量要足够多
被考察对象之间的差异要足够大
- 从若干个别性前提得出全称性结论的推理
- 穆勒五法
- 求同法:也叫契合法,其基本内容是:在被研究的现象a出现的若干个场合中,只有一个先行情况是相同的,那么,这个相同的先行情况就是被研究现象a的原因
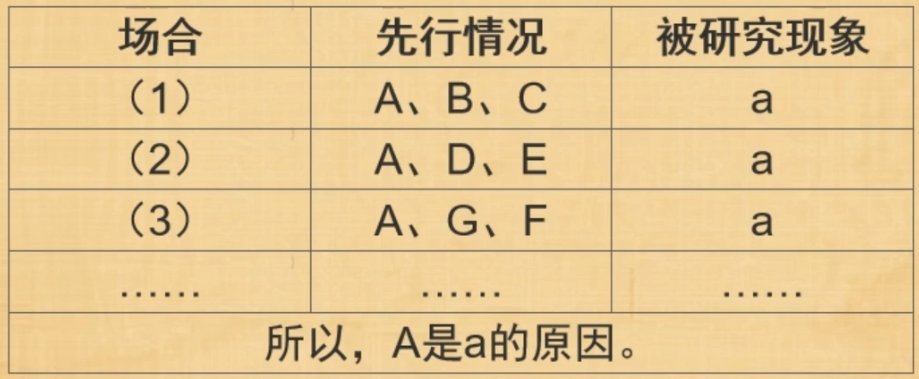
- 求异法:又叫差异法,其基本内容是:在被研究现象出现和不出现的两个场合,只有一个先行情况是不同的,其余都相同;并且,当这个不同的先行情况出现时,被研究现象a出现,否则a不出现。那么,这个不同的先行情况就是被研究现象a的原因

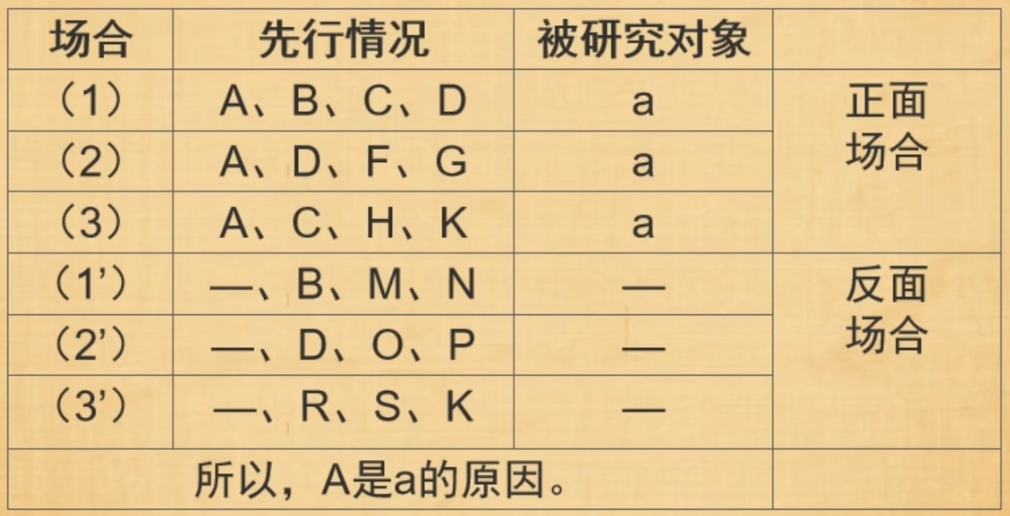
- 求同求异并用法:也叫契合差异并用法,其基本内容是:在若干正面场合中,都有一个相同的先行情况出现;而在若干反面场合中,该先行情况不出现。那么,该先行情况就是被研究现象a的原因
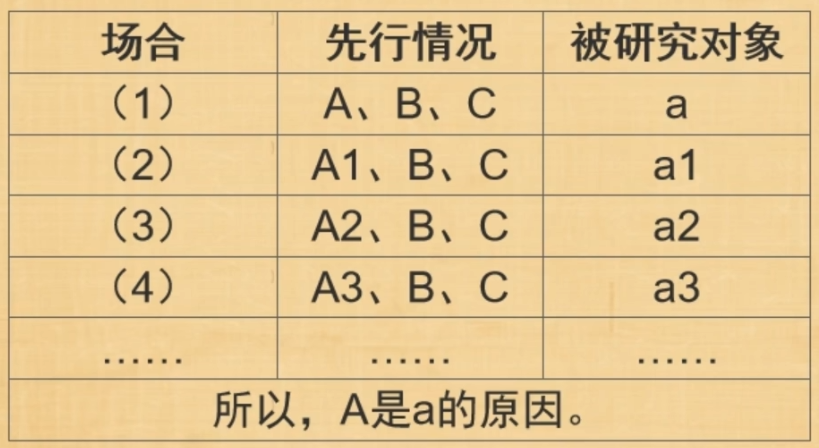
- 共变法:是指如果在被研究现象a发生某种程度变化的各个场合中,只有一个先行情况有量的变化,而其他先行情况都不变,那么,这唯一发生变化的先行情况就是a的原因。
- 剩余法:是指如果已知某复合情况是另一复杂现象的原因,同时又知该复合情况中某一部分是另一复杂现象中某一部分的原因,那么,该复合情况的其余部分就是另一复杂现象的其余部分的原因。

- 求同法:也叫契合法,其基本内容是:在被研究的现象a出现的若干个场合中,只有一个先行情况是相同的,那么,这个相同的先行情况就是被研究现象a的原因
- 类比推理
- 类比推理是根据两个或两类事物在某些属性上相同,推断它们在另外的属性上也相同的一种归纳推理

- 类比推理是根据两个或两类事物在某些属性上相同,推断它们在另外的属性上也相同的一种归纳推理
逻辑规律
- 矛盾律
- 在同一时间、同一方面,同一对象不能既具有又不具有某属性
- 排中律
- 在同一时间、同一方面,同一对象或者具有某属性,或者不具有该属性
- 同一律
- 在同一时间、同一方面,同一对象如果具有某属性,则就具有该属性
- 在同一时间、同一方面,同一组对象之间如果具有某关系,则就具有该关系